12-20 22:52:45 浏览次数:712次 栏目:高二数学辅导

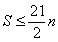

从而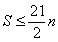 .
.
四、解:存在.用数学归纳法证明它的加强命题:对任何正整数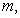 存在
存在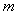 个连续的整数,使得每一个都含有重复的素因子.
个连续的整数,使得每一个都含有重复的素因子.
当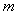 =1时,显然成立.这只需取一个素数的平方.
=1时,显然成立.这只需取一个素数的平方.
假设当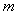 =
=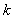 时命题成立,即有
时命题成立,即有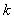 个连续整数
个连续整数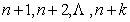 ,它们分别含有重复的素因子
,它们分别含有重复的素因子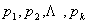 ,任取一个与
,任取一个与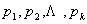 都不同的素数
都不同的素数 (显然存在),当
(显然存在),当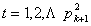 时,
时,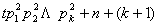 这
这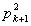 个数中任两个数的差是形如
个数中任两个数的差是形如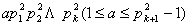 的数,不能被
的数,不能被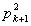 整除,故这
整除,故这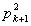 个数除以
个数除以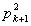 后,余数两两不同.但除以
后,余数两两不同.但除以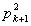 后的余数只有0,1,…,
后的余数只有0,1,…,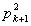 -1这
-1这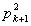 个,从而恰有一个数
个,从而恰有一个数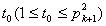 ,使
,使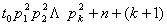 能被
能被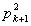 整除.这时,(
整除.这时,(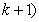 个连续整数:
个连续整数: 
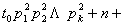 2,…,
2,…,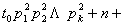
 ,
,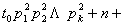 (
( +1)分别能被
+1)分别能被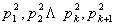 整除,即
整除,即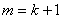 时命题成立.故题对一切正整数
时命题成立.故题对一切正整数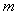 均成立.
均成立.
tag: 数学 高二数学辅导,高二数学辅导资料,高二学习方法,高中学习 - 高二学习 - 高二数学 - 高二数学辅导
相关分类
高二数学辅导 推荐