12-20 22:52:45 浏览次数:712次 栏目:高二数学辅导
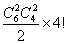 种,所以概率是
种,所以概率是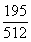 .
.
9.解:( 1)由题设知F(1,0)且直线AB的斜率存在,设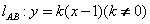 ,代入
,代入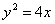 ,
,
得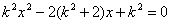 , 得
, 得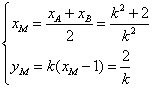 ,
, 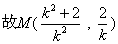 .
.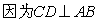 ,所以
,所以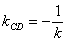 , 同理可
, 同理可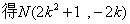 ,
,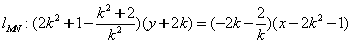
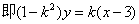 ,故不论k为何值,直线MN恒过定点T(3,0) .
,故不论k为何值,直线MN恒过定点T(3,0) .
( 2)由抛物线定义可知,圆M、圆N都与抛物线的准线x= -1 相切,所以圆M、圆N的半径分别为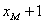 、
、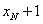 ,从而,⊙
,从而,⊙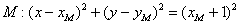
⊙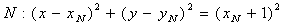
由-得公共弦所在直线方程为:
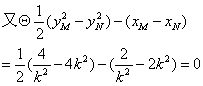
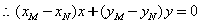
故:两圆相交弦所在的直线经过原点.
www.170xue.com
10.解:(1)设方程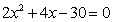 的两个实根为
的两个实根为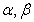 ,则
,则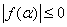 ,从而
,从而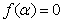 ,同理
,同理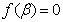 ,
,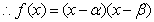 ,由韦达定理:
,由韦达定理: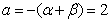 ,
,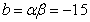 .
.
(2)由(1)知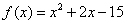 ,从而
,从而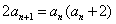 ,即
,即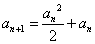
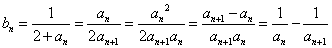 ,
,
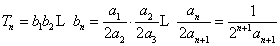 ,
,
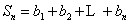
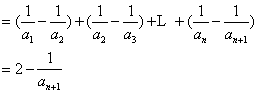 ,故
,故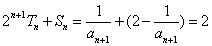
tag: 数学 高二数学辅导,高二数学辅导资料,高二学习方法,高中学习 - 高二学习 - 高二数学 - 高二数学辅导
相关分类
高二数学辅导 推荐