12-20 22:52:45 浏览次数:712次 栏目：高二数学辅导
所以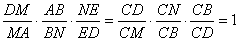
，
于是由塞瓦定理可知
、
、
相交于点P.
又
⊥
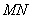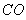，所以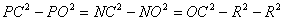
，
即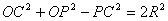
.
二、证明：设分为三个集合A、B、C.
假设A中无距离为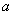
的点，B中无距离为
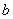的点， C中无距离为
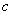的点。
不妨设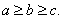
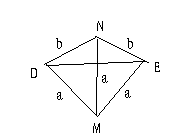从A中任取一点M，以M为球心作半径为
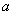的球面
，该球面上的点属于B或C，若这些点全在C中，则其中必有2点距离为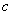
，矛盾！故该球面上有一点N
B，以N为球心，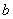
为半径的球面
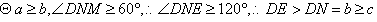与
相交于一个圆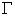
，设其直径为DE。
如图所示，
.
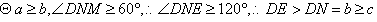而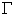
上的点只能属于C，在
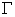上存在两点距离为C，这就与假设矛盾！
三、解：
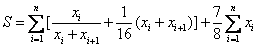
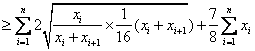
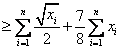
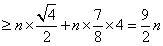
当且仅当
时(i=1，2，
，n)，取得等号．
另一方面，当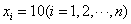
时，S=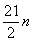
，下面我们来证明它是最大的
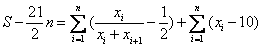
tag: 数学 高二数学辅导，高二数学辅导资料,高二学习方法，高中学习 - 高二学习 - 高二数学 - 高二数学辅导
相关分类
高二数学辅导 推荐
