12-20 22:51:02 浏览次数:242次 栏目:初三数学试题
圆形练习题及答案(六)
一、选择题
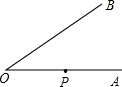
1. (2001江苏苏州3分)如图,已知∠AOB=30°,P为边OA上一点,且OP=5 cm,若以P为圆心,r为半径的圆与OB相切,则半径r为【 】
A.5cm B.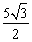 cm C.
cm C.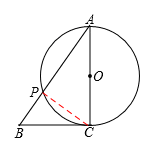 cm D.
cm D.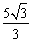 cm
cm
【答案】C。
【考点】直线与圆的位置关系,含30度角直角三角形的性质。
【分析】作PD⊥OB于D,

∵在直角三角形POD中,∠AOB=30°,P为边OA上一点,且OP=5cm,
∴PD=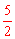 (cm)。
(cm)。
∵根据直线和圆相切,则圆的半径等于圆心到直线的距离,
∴r=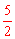 cm。故选C。
cm。故选C。
2. (2001江苏苏州3分)如图,在△ABC中,∠C=90°,AB=10,AC=8,以AC为直径作圆与斜边交于点P,则BP的长为【 】

A.6.4 B.3.2 C.3.6 D.8
【答案】C。
【考点】圆周角定理,相似三角形的判定和性质。
【分析】连接PC,
∵AC是直径,∴∠APC=90°。
∵在△ABC中,∠C=90°,AB=10,AC=8,∴∠APC=∠ACB=90°。

∵∠A=∠A,∴△APC∽△ACB。∴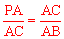 ,即
,即 。
。
∴PA=6.4。∴PB=AB-PA=10-6.4=3.6。故选C。
3.(江苏省苏州市2002年3分)如图,⊙O的弦AB=8cm,弦CD平分AB于点E。若CE=2 cm,则ED长为【 】
A. 8cm B. 6cm C. 4cm D. 2cm
【答案】A。

【考点】相交弦定理
【分析】根据相交弦定理求解:根据相交弦定理,得AE•BE=CE•ED,即ED=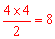 (cm)。故选A。
(cm)。故选A。
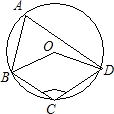
4.(江苏省苏州市2002年3分) 如图,四边形ABCD内接于⊙O,若∠BOD=1600,则∠BCD=【 】
A. 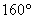 B.
B. 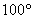 C.
C.  D.
D. 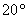
【答案】B。
【考点】圆内接四边形的性质,圆周角定理。
【分析】根据同弧所对的圆周角与圆心角的关系,易求得圆周角∠BAD的度数;由于圆内接四边形的内对角互补,则∠BAD+∠BCD=180°,由此得解:
∵四边形ABCD内接于⊙O,∴∠BAD+∠BCD=180°。
又∵∠BAD=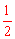 ∠BOD=80°,∴∠BCD=180°-∠BAD=100°。
∠BOD=80°,∴∠BCD=180°-∠BAD=100°。
故选B。
5.(江苏省苏州市2002年3分)如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D。DF⊥AC,垂足为F,DE⊥BC,垂足为E。

给出下列4个结论:
①CE=CF,②∠ACB=∠EDF ,③DE是⊙O的切线,④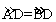 。
。
其中一定成立的是【 】
A. ①②③ B. ②③④ C. ①③④ D. ①②④
【答案】D。
【考点】角平分线的性质,全等三角形的判定和性质,平角定义,四边形内角和定理,切线的判定,圆周角定理。
【分析】①∵CD是∠ACE的平分线,∴∠DCE=∠DCF。
∵DF⊥AC,DE⊥BC,∴∠DEC=∠DFC=900。
又∵DC=DC,∴△CDE≌△CDF(AAS)。∴CE=CF。∴①正确。
②∵根据四边形内角和定理∠ACE+∠EDF+∠DEC+∠DFC=3800和∠DEC=∠DFC=900,
 ∴∠ACE+∠EDF=180°。
∴∠ACE+∠EDF=180°。
tag: 练习题 初三数学试题,九年级数学试题,初中数学学习方法,初中学习 - 初三学习 - 初三数学 - 初三数学试题
相关分类
初三数学试题 推荐