12-20 22:51:02 浏览次数:520次 栏目:初三数学试题
∵ AB⊥CD,∴ ∠C=30°,∴ ∠ADC=60°.
点拨:直径所对的圆周角等于90°,在同一个圆中,同一条弧所对
的圆心角等于圆周角的2倍.
20. 解:连接AE,则AE⊥BC.由于E是BC的中点,则AB=AC,∠BAE=∠CAE,则BE=DE=EC,S弓形BE=S弓形DE,∴ S阴影=S△DCE.由于∠BED=120°,则△ABC与△DEC都是等边三角形,∴ S△DCE= ×2×
×2×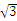 =
=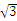 .
.
21.分析:(1)欲求∠DEB,已知一圆心角,可利用圆周角与圆心角的关系求解.
(2)利用垂径定理可以得到 ,从而
,从而 的长可求.
的长可求.
解:(1)连接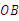 ,∵
,∵ 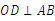 ,∴
,∴  ,弧AD=弧BD,
,弧AD=弧BD,
∴ 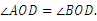 又
又 ,
,
 ∴
∴ 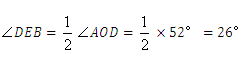 .
.
(2)∵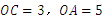 ,∴
,∴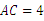 .
.
又 ,∴
,∴ 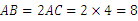 .
.
22.分析:要证明△OEF是等腰三角形,可以转化为证明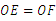 ,通过证明△OCE≌△ODF即可得出.
,通过证明△OCE≌△ODF即可得出.
证明:如图,连接OC、OD,则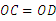 ,
,
∴ ∠OCD=∠ODC.
在△OCE和△ODF中,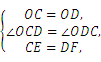
∴△OCE≌△ODF(SAS),
∴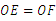 ,从而△OEF是等腰三角形.
,从而△OEF是等腰三角形.
23.分析:由圆周角定理,得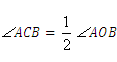 ,
,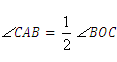 ;已知
;已知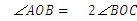 ,联立三式可得.
,联立三式可得.
解: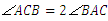 .理由如下:
.理由如下:
∵ 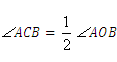 ,
,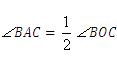 ,
,
又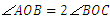 ,∴
,∴ 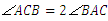 .
.
24.解:(1)已知桥拱的跨度AB=16米,拱高CD=4米,
∴ AD=8米.利用勾股定理可得
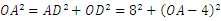 ,解得OA=10(米).
,解得OA=10(米).
故桥拱的半径为10米.
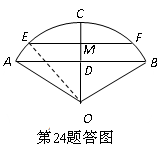 (2)当河水上涨到EF位置时,因为
(2)当河水上涨到EF位置时,因为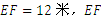 ∥
∥
tag: 练习题 初三数学试题,九年级数学试题,初中数学学习方法,初中学习 - 初三学习 - 初三数学 - 初三数学试题
相关分类
初三数学试题 推荐