12-20 22:51:02 浏览次数:520次 栏目:初三数学试题
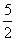 ,所以OP<OC,即点P在⊙O内.
,所以OP<OC,即点P在⊙O内.
9.C 解析:设圆心角为n°,则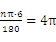 ,解得n=120.
,解得n=120.
10.C 解析: 第一次转动是以点B为圆心,AB为半径,圆心角是90度,所以弧长= ,第二次转动是以点C为圆心,A1C为半径,圆心角为60度,所以弧长=
,第二次转动是以点C为圆心,A1C为半径,圆心角为60度,所以弧长=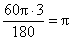 ,所以走过的路径长为
,所以走过的路径长为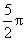 +
+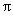 =
=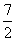
 (cm).
(cm).
二、填空题
11. 2 解析:∵ BC =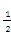 AB=
AB=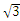 ,∴ OB=
,∴ OB= =
= =2.
=2.
12. 60 解析:∵ 四边形OABC为平行四边形,∴ ∠B=∠AOC,∠BAO=∠BCO.
∵  =2∠D,∠B+∠D=180°,∴ ∠B=∠AOC=120°,∠BAO=∠BCO=60°.
=2∠D,∠B+∠D=180°,∴ ∠B=∠AOC=120°,∠BAO=∠BCO=60°.
又∵ ∠BAD+∠BCD=180°,∴ ∠OAD+∠OCD=(∠BAD+∠BCD)-(∠BAO+∠BCO)=180°-120°=60°.
13.40° 解析:因为∠AOC=100°,所以∠BOC=80°.又∠D=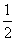 ∠BOC,所以∠D=40°.
∠BOC,所以∠D=40°.
14.8;2 解析:因为OD⊥AB,由垂径定理得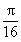 ,故
,故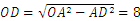 ,
, .
.
15.55° 解析:根据同弧所对的圆周角等于圆心角的一半可得.
16. 4︰1 解析:由题意知,小扇形的弧长为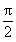 ,则它组成的圆锥的底面半径=
,则它组成的圆锥的底面半径=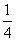 ,小圆锥的底面面积=
,小圆锥的底面面积=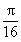 ;大扇形的弧长为π,则它组成的圆锥的底面半径=
;大扇形的弧长为π,则它组成的圆锥的底面半径=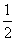 ,大圆锥的底面面积=
,大圆锥的底面面积=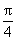 ,∴大圆锥的底面面积︰小圆锥的底面面积=4︰1.
,∴大圆锥的底面面积︰小圆锥的底面面积=4︰1.
17.250 解析:依据垂径定理和勾股定理可得.
18. 4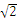 解析:扇形的弧长l=
解析:扇形的弧长l=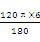 =4π(cm),所以圆锥的底面半径为4π÷2π=2(cm),所以这个圆锥形纸帽的高为
=4π(cm),所以圆锥的底面半径为4π÷2π=2(cm),所以这个圆锥形纸帽的高为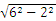 = 4
= 4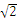 (cm).
(cm).
三、解答题
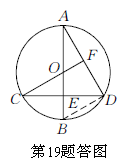 19.分析:连接BD,易证∠BDC=∠C,∠BOC=2∠BDC=2∠C,∴ ∠C=
19.分析:连接BD,易证∠BDC=∠C,∠BOC=2∠BDC=2∠C,∴ ∠C=
30°, 从而∠ADC=60°.
解:连接BD.∵ AB是⊙O的直径,∴ BD⊥AD.
又∵ CF⊥AD,∴ BD∥CF.∴ ∠BDC=∠C.
又∵ ∠BDC= ∠BOC,∴ ∠C=
∠BOC,∴ ∠C=
tag: 练习题 初三数学试题,九年级数学试题,初中数学学习方法,初中学习 - 初三学习 - 初三数学 - 初三数学试题
相关分类
初三数学试题 推荐