圆形练习题及答案（三）

标签：九年级数学试题,初中数学学习方法,http://www.170xue.com 圆形练习题及答案（三）,http://www.170xue.com
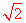），B（，0）。∴OA=OB= 2 。

∴△AOB是等腰直角三角形。∴AB=2，

过点O作OD⊥AB，则OD=BD=AB=×2=1。

又∵⊙O的半径为1，∴圆心到直线的距离等于半径。

∴直线y=x- 2 与⊙O相切。故选B。

7.（2012四川巴中3分）已知两圆的半径分别为1和3，当这两圆内含时，圆心距d的范围是（　　）

A. 0　B.0≤d＜3　　C.0≤d＜2　　D.0≤d＜3－1

【答案】D。

【考点】圆与圆的位置关系。

【分析】根据两圆的位置关系的判定：外切（两圆圆心距离等于两圆半径之和），内切（两圆圆心距离等于两圆半径之差），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）。因此，

由题意知，两圆内含，则0≤d＜3－1。故选D。

8.（2012四川自贡3分）如图，圆锥形冰淇淋盒的母线长是13cm，高是12cm，则该圆锥形底面圆的面积是（　　）

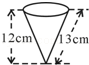A．10πcm2　　B．25πcm2　　C．60πcm2　　　D．65πcm2

【答案】B。

【考点】圆锥的计算，勾股定理。菁优网版权所有

【分析】如图，在Rt△AOB中，圆锥的母线长AB=13cm，圆锥的OB=高12cm，

∴圆锥的底面半径（cm），

∴S =π×52=25π（cm2）。故选B。

9.（2012四川泸州2分）如图，在△ABC中，AB为⊙O的直径，∠B = 60°，∠BOD = 100°，则∠C的

度数为（　　）

A、50°　　　B、60°　　　C、70°　　D、80°

【答案】C。

【考点】圆周角定理，三角形的内角和定理。

【分析】∵∠BOD＝100°，∴∠A＝∠BOD＝50°。

∵∠B＝60°，∴∠C=180°－∠A－∠B=70°。故选C。

10.（2012四川南充3分）一个圆锥的侧面积是底面积的2倍。则圆锥侧面展开图的扇形的圆心角是（　　）　

A .1200　　　B.1800　　　C.2400　　　D.3000

【答案】B。

【考点】圆锥的计算，扇形的弧长。

【分析】设母线长为R，底面半径为r，

∴底面周长=2πr，底面面积=πr2，侧面面积=πrR.

∵侧面积是底面积的2倍，∴R=2r。

设圆心角为n，有，∴n=180°。故选B。

二、填空题

1.（2012四川成都4分）如图，AB是⊙O的弦，OC⊥AB于C．若AB=，0C=1，则半径OB的长为▲　　．

【答案】2。

【考点】垂径定理，勾股定理。

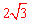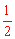【分析】∵AB是⊙O的弦，OC⊥AB于C，AB=，∴BC=AB=。

∵OC=1，∴在Rt△OBC中，。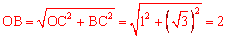

2.（2012四川成都4分）一个几何体由圆锥和圆柱组成，其尺寸如图所示，则该几何体的全面积(即表面积)为　　▲　　 (结果保留π)

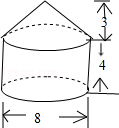
【答案】68π。

【考点】圆锥和圆柱的计算，勾股定理。

【分析】圆锥的母线长是：。

∴圆锥的侧面积是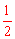：×8π×5=20π，

圆柱的侧面积是：8π×4=32π．

几何体的下底面面积是：π×42=16π。

∴该几何体的全面积（即表面积）为：20π+32π+16π=68π。

3.（2012四川乐山3分）如图，⊙O是四边形ABCD的内切圆，E、F、G、H是切点，点P是优弧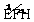上异于E、H的点．若∠A=50°，则∠EPH=　▲ 　．

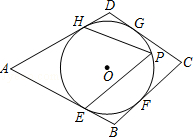
【答案】65°。

【考点】切线的性质，圆周角定理。

【分析】如图，连接OE，OH，

∵⊙O是四边形ABCD的内切圆，E、F、G、H是切点，

∴∠OEA=∠OHA=90°。

又∵∠A=50°，

∴∠EOH=360°﹣∠OEA﹣∠OHA﹣∠A=360°﹣90°﹣90°﹣50°=130°。

又∵∠EPH和∠EOH分别是

上一页  [1] [2] [3] [4] [5] [6] [7] [8] [9] [10]  下一页

，圆形练习题及答案（三）