12-20 22:52:45 浏览次数:881次 栏目:高考数学复习
所以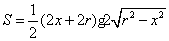
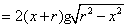 ,其定义域为
,其定义域为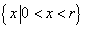 .
.
(II)记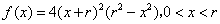 , 则
, 则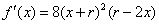 .
.
令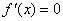 ,得
,得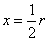 .因为当
.因为当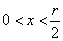 时,
时,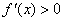 ;当
;当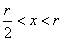 时,
时,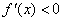 ,
,
所以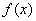 在
在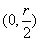 上是单调递增函数,在
上是单调递增函数,在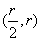 上是单调递减函数,所以
上是单调递减函数,所以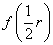 是
是 的最大值.因此,当
的最大值.因此,当 时,
时,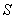 也取得最大值,最大值为
也取得最大值,最大值为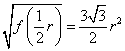 .即梯形面积
.即梯形面积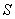 的最大值为
的最大值为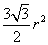 .
.
7.设函数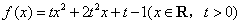 .
.
(Ⅰ)求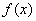 的最小值
的最小值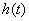 ;
;
(Ⅱ)若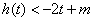 对
对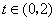 恒成立,求实数
恒成立,求实数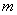 的取值范围.
的取值范围.
解:(Ⅰ)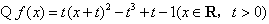 ,
,
 当
当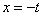 时,
时,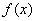 取最小值
取最小值 ,即
,即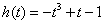 .
.
(Ⅱ)令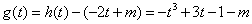 ,
,
由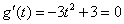 得
得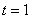 ,
,
tag: 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐