12-20 22:58:55 浏览次数:572次 栏目:高考数学复习
2013高考数学复习:圆锥曲线(二)
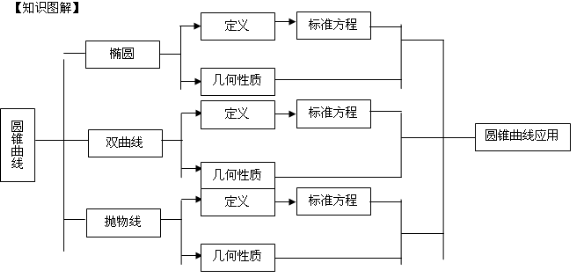
【方法点拨】
解析几何是高中数学的重要内容之一,也是衔接初等数学和高等数学的纽带。而圆锥曲线是解析几何的重要内容,因而成为高考考查的重点。研究圆锥曲线,无外乎抓住其方程和曲线两大特征。它的方程形式具有代数的特性,而它的图像具有典型的几何特性,因此,它是代数与几何的完美结合。高中阶段所学习和研究的圆锥曲线主要包括三类:椭圆、双曲线和抛物线。圆锥曲线问题的基本特点是解题思路比较简单清晰,解题方法的规律性比较强,但是运算过程往往比较复杂,对学生运算能力,恒等变形能力,数形结合能力及综合运用各种数学知识和方法的能力要求较高。
1. 一要重视定义,这是学好圆锥曲线最重要的思想方法,二要数形结合,既熟练掌握方程组理论,又关注图形的几何性质.
2.着力抓好运算关,提高运算与变形的能力,解析几何问题一般涉及的变量多,计算量大,解决问题的思路分析出来以后,往往因为运算不过关导致半途而废,因此要寻求合理的运算方案,探究简化运算的基本途径与方法,并在克服困难的过程中,增强解决复杂问题的信心,提高运算能力.
3.突出主体内容,要紧紧围绕解析几何的两大任务来学习:一是根据已知条件求曲线方程,其中待定系数法是重要方法,二是通过方程研究圆锥曲线的性质,往往通过数形结合来体现,应引起重视.
4.重视对数学思想如方程思想、函数思想、数形结合思想的归纳提炼,达到优化解题思维、简化解题过程
第2课 椭圆B
【考点导读】
1. 掌握椭圆的第二定义,能熟练运用两个定义解决椭圆的有关问题;
2. 能解决椭圆有关的综合性问题.
【基础练习】
1.曲线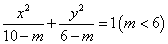 与曲线
与曲线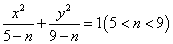 的(D)
的(D)
A 焦点相同 B 离心率相等 C准线相同 D 焦距相等
2.如果椭圆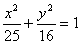 上的点A到右焦点的距离等于4,那么点A到两条准线的距离分别是
上的点A到右焦点的距离等于4,那么点A到两条准线的距离分别是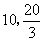
3 离心率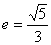 ,一条准线为
,一条准线为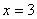 的椭圆的标准方程是
的椭圆的标准方程是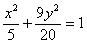
 【范例导析】
【范例导析】
例1.椭圆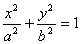 (a>b>0)的二个焦点F1(-c,0),F2(c,0),M是椭圆上一点,且
(a>b>0)的二个焦点F1(-c,0),F2(c,0),M是椭圆上一点,且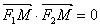 。求离心率e的取值范围.
。求离心率e的取值范围.
分析:离心率与椭圆的基本量a、b、c有关,所以本题可以用基本量表示椭圆上点的坐标,再借助椭圆椭圆上点坐标的范围建立关于基本量的不等式,从而确定离心率的范围.
解:设点M的坐标为(x,y),则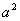 ,
,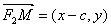 。由
。由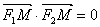 ,得x2-c2+y2=0,即x2-c2=-y2。 ①
,得x2-c2+y2=0,即x2-c2=-y2。 ①
又由点M在椭圆上,得y2=b2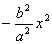 ,代入①,得x2-c2
,代入①,得x2-c2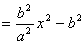 ,即
,即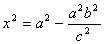 。
。
∵0≤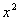 ≤
≤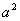 ,∴0≤
,∴0≤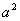
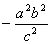 ≤
≤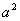 ,即0≤
,即0≤
tag: 圆锥曲线 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐