12-20 22:52:45 浏览次数:881次 栏目:高考数学复习
解:设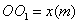 ,则由题设可得正六棱锥底面边长为
,则由题设可得正六棱锥底面边长为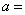
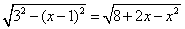 (单位:m)。
(单位:m)。
于是底面正六边形的面积为(单位:m2):
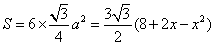
帐篷的体积为(单位:m3):
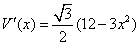
求导数,得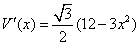 ;
;
令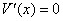 解得x=-2(不合题意,舍去),x=2。
解得x=-2(不合题意,舍去),x=2。
当1
所以当x=2时,V(x)最大。
答:当OO1为2m时,帐篷的体积最大。
点评:本题是结合空间几何体的体积求最值,加深理解导数的工具作用,主要考查利用导数研究函数的最大值和最小值的基础知识,以及运用数学知识解决实际问题的能力。
【反馈演练】
1.设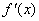 是函数
是函数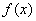 的导函数,将
的导函数,将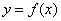 和
和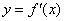 的图象画在同一个直角坐标系中,不可能正确的是 图4 。
的图象画在同一个直角坐标系中,不可能正确的是 图4 。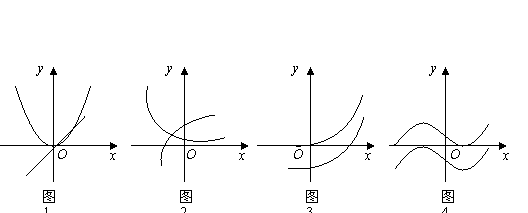
2.已知二次函数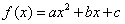 的导数为
的导数为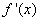 ,
,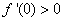 ,对于任意实数
,对于任意实数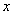 都有
都有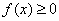 ,则
,则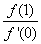 的最小值为
的最小值为 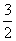 。
。
3.若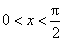 ,则下列命题正确的是 (3) .
,则下列命题正确的是 (3) .
(1)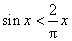 (2)
(2) (3)
(3)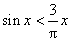 (4)
(4)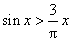
4.函数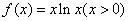 的单调递增区间是
的单调递增区间是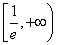 .
.
5.已知函数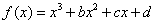 的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为
的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为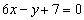 .
.
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)求函数y=f(x)的单调区间.
,2017高考数学复习:导数的应用tag: 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐