12-20 22:53:02 浏览次数:534次 栏目:高考数学复习
解:(Ⅰ)因为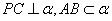 ,所以
,所以 .
.
同理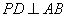 .
.
又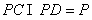 ,故
,故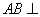 平面
平面 .
.
(Ⅱ)平面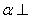 平面
平面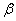 。证明如下:设
。证明如下:设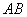 与平面
与平面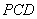 的交点为
的交点为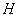 ,
,
连结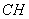 、
、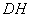 .因为
.因为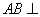 平面
平面 ,所以
,所以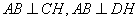 ,
,
所以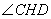 是二面角
是二面角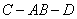 的平面角.
的平面角.
又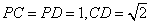 ,所以
,所以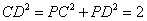 ,即
,即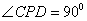 .
.
在平面四边形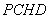 中,
中,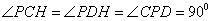 ,
,
所以 .故平面
.故平面 平面
平面 .
.
【反馈演练】
1.判断题(对的打“√”,错的打“×”)
(1)垂直于两条异面直线的直线有且只有一条 ( )
(2)两线段AB、CD不在同一平面内,如果AC=BD,AD=BC,则AB⊥CD( )
(3)在正方体中,相邻两侧面的一对异面的对角线所成的角为60º ( )
(4)四边形的一边不可能既和它的邻边垂直,又和它的对边垂直 ( )
答案:(1)× (2)× (3)√ (4)×
2.定点P不在△ABC所在平面内,过P作平面α,使△ABC的三个顶点到α的距离相等,这样的平面共有 4 个。
3.给出以下四个命题:(1)若空间四点不共面,则其中无三点共线;(2)若直线上有一点在平面外,则该直线在平面外;(3)若直线a,b,c中,a与b共面且b与c共面,则a与c共面;(4)两两相交的三条直线共面。其中所有正确命题的序号是 (1)(2) 。
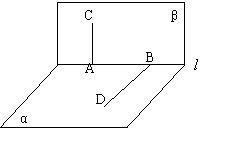
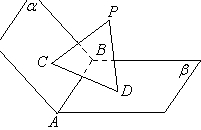
4.如图,已知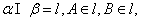 (A,B不重合)过A在平面α内作直线AC,过B在平面β内作直线BD。求证:AC和BD是异面直线。证明:(反证法)若AC和BD不是异面直线,
(A,B不重合)过A在平面α内作直线AC,过B在平面β内作直线BD。求证:AC和BD是异面直线。证明:(反证法)若AC和BD不是异面直线,
设确定平面γ,则由题意可知:平面α和γ都过AC和AC外一点B,所以两平面重合。
同理可证平面β和γ也重合,所以平面α和β也重合。
这与已知条件平面α和β相交矛盾。
所以AC和BD是异面直线。
,2017高考数学复习:立体几何初步(二)tag: 高考数学 立体几何 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐