12-20 22:53:02 浏览次数:534次 栏目:高考数学复习
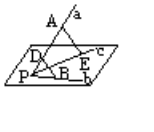
求证:BD和AE是异面直线
证明:假设__ 共面于?,则点A、E、B、D都在平面_ _内
?A?a,D?a,∴__?γ. ?P?a,∴P?__.
 ?P?b,B?b,P?c,E?c ∴_ _??, __??,这与____矛盾
?P?b,B?b,P?c,E?c ∴_ _??, __??,这与____矛盾
∴BD、AE__________
答案:假设BD、AE共面于?,则点A、E、B、D都在平面?内。
∵A?a,D?a,∴a??. ∵P?a,P??.
∵P?b,B?b,P?c,E?c. ∴ b??,c??,这与a、b、c不共面矛盾
∴BD、AE是异面直线 翰林
翰林

【范例导析】
例1.已知 ,从平面
,从平面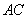 外一点
外一点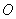 引向量
引向量
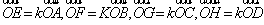 ,
,
(1)求证:四点 共面;(2)平面
共面;(2)平面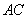
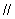 平面
平面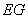 .
.
分析 :证明四点共面可以采用平面向量中的平面向量基本定理证明,
也可以转化为直线共面的条件即几何证法。
解:法一:(1)∵四边形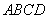 是平行四边形,∴
是平行四边形,∴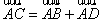 ,
,
∵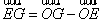 ,
,

∴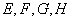 共面;
共面;
(2)∵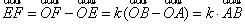 ,又∵
,又∵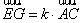 ,
,
∴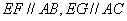
所以,平面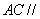 平面
平面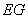 .
.
法二:(1)

∴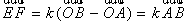
∴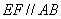
tag: 高考数学 立体几何 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐