12-20 22:53:02 浏览次数:534次 栏目:高考数学复习
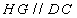 又
又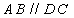 ∴
∴
∴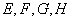 共面;
共面;
(2)由(1)知: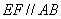 ,从而可证
,从而可证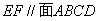
同理可证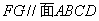 ,所以,平面
,所以,平面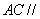 平面
平面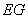 .
.
点评:熟练掌握定理是证明的关键,要学会灵活运用。
例2.已知空间四边形ABCD.
(1)求证:对角线AC与BD是异面直线;
(2)若AC⊥BD,E,F,G,H分别这四条边AB,BC,CD,DA的中点,试判断四边形EFGH的形状;
(3)若AB=BC=CD=DA,作出异面直线AC与BD的公垂线段.翰林汇
分析:证明两条直线异面通常采用反证法。
证明:(1)(反证法)假设AC与BD不是异面直线,则AC与BD共面,
所以A、B、C、D四点共面
这与空间四边形ABCD的定义矛盾
所以对角线AC与BD是异面直线
(2)解:∵E,F分别为AB,BC的中点,∴EF//AC,且EF= AC.
AC.
同理HG//AC,且HG= AC.∴EF平行且相等HG,∴EFGH是平行四边形.
AC.∴EF平行且相等HG,∴EFGH是平行四边形.
又∵F,G分别为BC,CD的中点,∴FG//BD,∴∠EFG是异面直线AC与BD所成的角.
∵AC⊥BD,∴∠EFG=90o.∴EFGH是矩形.
(3)作法取BD中点E,AC中点F,连EF,则EF即为所求.
点评:在空间四边形中我们通常会遇到上述类似的问题,取中点往往是很有效的方法,特别是遇到等腰三角形的时候。
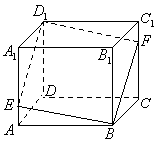
例3.如图,已知E,F分别是正方体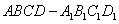 的棱
的棱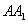 和棱
和棱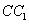 上的点,且
上的点,且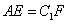 ,求证:四边形
,求证:四边形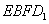 是平行四边形
是平行四边形
简证:由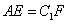 可以证得
可以证得 ≌
≌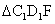
所以 又可以由正方体的性质证明
又可以由正方体的性质证明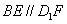
所以四边形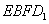 是平行四边形
是平行四边形
例4:如图,已知平面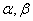 ,且
,且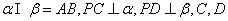 是垂足.
是垂足.
(Ⅰ)求证: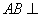 平面
平面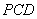 ;
;
(Ⅱ)若 ,试判断平面
,试判断平面 与平面
与平面
tag: 高考数学 立体几何 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐