12-20 22:52:45 浏览次数:213次 栏目:高二数学试题
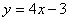 .wwW.x kB 1.c Om
.wwW.x kB 1.c Om
4. 5.
5.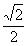 6. 9
6. 9
7.解(1)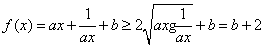 ,
,
当且仅当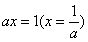 时,
时,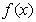 的最小值为
的最小值为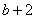
(2)由题意得: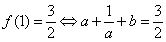 , ①
, ①
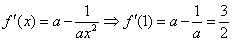 , ② 由①②得:
, ② 由①②得: 。
。
8.解(1)因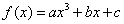 故
故 由于
由于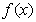 在点
在点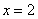 处取得极值
处取得极值
故有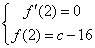 即
即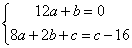 ,化简得
,化简得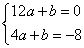 解得
解得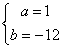
(2)由(1)知 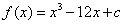 ,
,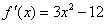
令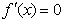 ,得
,得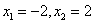 当
当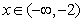 时,
时, 故
故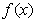 在
在 上为增函数;当
上为增函数;当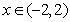 时,
时,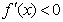 故
故 在
在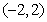 上为减函数
上为减函数
当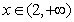 时
时 ,故
,故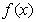 在
在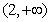 上为增函数。
上为增函数。
由此可知 在
在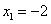
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] 下一页
,高二上册数学(文科)寒假作业及答案tag: 数学 高二数学试题,高二数学试题大全,高二学习方法,高中学习 - 高二学习 - 高二数学 - 高二数学试题
相关分类
高二数学试题 推荐