12-20 22:58:55 浏览次数:543次 栏目:高考数学试题
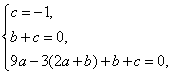
解得 ![]() .…………………………11 分
.…………………………11 分
所以函数的解析式为 ![]() .
.
又由( Ⅰ )知, ![]() 的单调增区间是( -∞ , -3 ) , ( 0 , +∞ ),单调减区间是( -3 , 0 ) .
的单调增区间是( -∞ , -3 ) , ( 0 , +∞ ),单调减区间是( -3 , 0 ) .
所以,函数 ![]() 的极大值为
的极大值为 ![]() . ……………….…14 分
. ……………….…14 分
5. 【北京市海淀区 2013 届高三上学期期末考试数学文】 (本小题 满分 13分) 已知函数 ![]() 与函数
与函数 ![]() 在点
在点 ![]() 处有公共的切线,设
处有公共的切线,设 ![]()
![]() .
.
( I ) 求 ![]() 的值
的值
( Ⅱ )求 ![]() 在 区间
在 区间 ![]() 上的最小值.
上的最小值.
【答案】解: (I)因为 ![]() 所以
所以 ![]() 在函数
在函数 ![]() 的图象上
的图象上
又 ![]() ,所以
,所以 ![]()
所以 ![]() ……………3分
……………3分
( Ⅱ )因为 ![]() ,其定义域为
,其定义域为 ![]()
![]() ………5分
………5分
当 ![]()
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] 下一页
,高考数学知识点试题解析:导数tag: 知识点 高考数学 高考数学试题,高考数学试题大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学试题
相关分类
高考数学试题 推荐