12-20 22:53:02 浏览次数:147次 栏目:高考数学复习
分析:利用函数的有界性求解.
解法一:原式可化为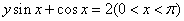 ,得
,得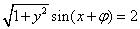 ,即
,即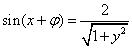 ,
,
故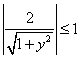 ,解得
,解得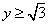 或
或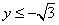 (舍),所以
(舍),所以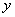 的最小值为
的最小值为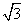 .
.
解法二: 表示的是点
表示的是点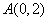 与
与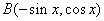 连线的斜率,其中点B在左半圆
连线的斜率,其中点B在左半圆 上,由图像知,当AB与半圆相切时,
上,由图像知,当AB与半圆相切时,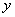 最小,此时
最小,此时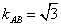 ,所以
,所以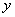 的最小值为
的最小值为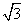 .
.
点评:解法一利用三角函数的有界性求解;解法二从结构出发利用斜率公式,结合图像求解.
www.170xue.com
例3.已知函数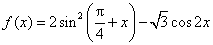 ,
,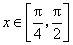 .
.
(I)求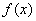 的最大值和最小值;
的最大值和最小值;
(II)若不等式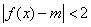 在
在 上恒成立,求实数
上恒成立,求实数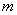 的取值范围.
的取值范围.
分析:观察角,单角二次型,降次整理为 形式.
形式.
解:(Ⅰ)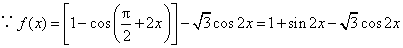
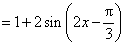 .
.
又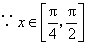 ,
,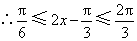 ,即
,即 ,
,
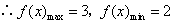 .
.
(Ⅱ)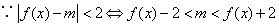 ,
,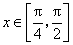 ,
,
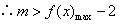 且
且 ,
,

tag: 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐