12-20 22:52:45 浏览次数:132次 栏目:高考数学复习
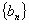 的前
的前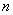 项和
项和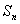 ;
;
(Ⅲ)设 ,数列
,数列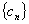 的前
的前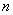 项和为
项和为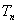 .求证:对任意的
.求证:对任意的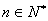 ,
,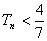 .
.
分析:本题所给的递推关系式是要分别“取倒”再转化成等比型的数列,对数列中不等式的证明通常是放缩通项以利于求和。
解:(Ⅰ)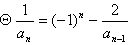 ,
,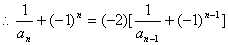 ,
,
又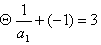 ,
, 数列
数列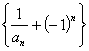 是首项为
是首项为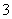 ,公比为
,公比为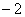 的等比数列.
的等比数列.
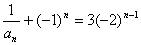 , 即
, 即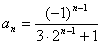 .
.
(Ⅱ)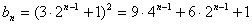 .
.
 .
.
(Ⅲ)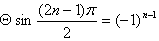 ,
, 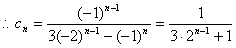 .
.
当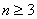 时,则
时,则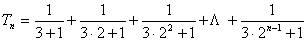
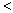
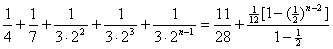
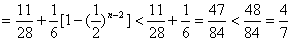 .
.
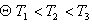 ,
,  对任意的
对任意的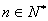 ,
,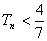 .
.
点评:本题利用转化思想将递推关系式转化成我们熟悉的结构求得数列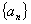 的通项
的通项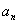 ,第二问分组求和法是非常常见的方法,第三问不等式的证明要用到放缩的办法,放缩的目的是利于求和,所以通常会放成等差、等比数列求和,或者放缩之后可以裂项相消求和。
,第二问分组求和法是非常常见的方法,第三问不等式的证明要用到放缩的办法,放缩的目的是利于求和,所以通常会放成等差、等比数列求和,或者放缩之后可以裂项相消求和。
【反馈演练】
1.已知数列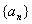
tag: 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐