12-20 22:53:02 浏览次数:837次 栏目:高考数学复习
 或
或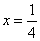 .
.
而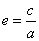 ,有
,有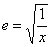 .故
.故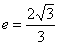 或
或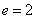 .
.
因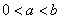 ,故
,故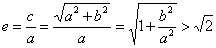 ,
,
所以应舍去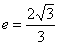 .故所求离心率
.故所求离心率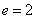 .
.
说明:此题易得出错误答案: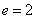 或
或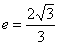 .其原因是未注意到题设条件
.其原因是未注意到题设条件 ,从而离心率
,从而离心率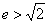 .而
.而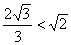 ,故应舍去.
,故应舍去.
8.已知双曲线的中心在原点,焦点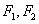 在坐标轴上,离心率为
在坐标轴上,离心率为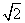 ,且过点
,且过点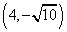 .
.
(1)求双曲线方程;(2)若点 在双曲线上,求证:
在双曲线上,求证: ;
;
(3)对于(2)中的点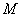 ,求
,求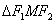 的面积.
的面积.
解:(1)由题意,可设双曲线方程为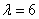 ,又双曲线过点
,又双曲线过点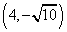 ,解得
,解得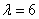
∴ 双曲线方程为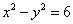 ;
;
(2)由(1)可知,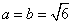 ,
, , ∴
, ∴ 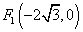 ,
,
∴  ,
, , ∴
, ∴ 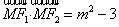 ,
,
又点
tag: 圆锥曲线 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐