12-20 22:58:55 浏览次数:994次 栏目：高考数学复习
又
，∴
∴椭圆的方程为
.
②若焦点在y轴上，设方程为
，
∵点P（3，0）在该椭圆上∴
即
又，∴
∴椭圆的方程为
方法二：设椭圆方程为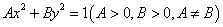
.∵点P（3，0）在该椭圆上∴9A=1，即
，又∴，∴椭圆的方程为或.
【点拨】求椭圆标准方程通常采用待定系数法，若焦点在x轴上，设方程为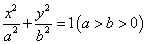
，若焦点在y轴上，设方程为，有时为了运算方便，也可设为
，其中
.
例2.点A、B分别是椭圆
长轴的左、右端点，点F是椭圆的右焦点，点P在椭圆上，且位于
轴上方，
。
（1）求点P的坐标；
（2）设M是椭圆长轴AB上的一点，M到直线AP的距离等于
，求椭圆上的点到点M的距离
的最小值。
【分析】①列方程组求得P坐标；②解几中的最值问题通常可转化为函数的最值来求解，要注意椭圆上点坐标的范围.
解：（1）由已知可得点A(－6，0)，F(0，4)
设点P(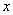
，
)，则
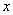=（+6，），
=（
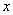
tag: 圆锥曲线 高考数学 高考数学复习，高考数学复习大全,高考复习方法，高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐
