初二上册一次函数练习题及答案

标签：八年级数学试题,初中数学学习方法,http://www.170xue.com 初二上册一次函数练习题及答案,http://www.170xue.com
，化简得.

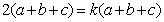　　分两种情况讨论：

　　当a+b+c≠0时，得k=2，此时直线是y=2x+3，过第一、二、三象限；

　　当a+b+c=0时，即a+b=-c，则k=-1，此时直线是y=-x，过第二、四象限．

　　综上所述，该直线必经过第二象限．

　　4.D【解析】设运输x吨货物，根据题意，
　　汽车运费：y=2x×120+5x×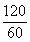+200=250x+200，
　　火车运费：y=1.8x×120+5x×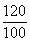+1600=222x+1600，

　　①250x+200=222x+1600，解得x=50，∴运输货物为50吨时，选择汽车与火车一样；

　　②250x+200＜222x+1600，解得x＜50，∴运输货物小于50吨时，选择汽车运输；

　　③250x+200＞222x+1600，解得x＞50，∴运输货物大于50吨时，选择火车运输．

　　综上所述，D选项符合．故选D．

　　5．解：(1)方案一：y=4x；

　　　　　　 　方案二：当0≤x≤3时，y=5x ；当x>3时，y=3×5+(x-3)×5×70%=3.5x+4.5.

　　　(2)设购买x千克的种子时，两种方案所付金额一样，则4x=3.5x+4.5，解这个方程得x=9，

　　　∴当购买9千克种子时，两种方案所付金额相同；当购买种子0＜x＜3时，方案一所付金额少，选择方案一；当购买种子3≤x＜9时，方案一所付金额少，选择方案一；当购买种子质量超过9千克时，方案二所付金额少，应选择方案二.

　　6．解：(1)填写表格如下：

运地收地	C	D	总计
A	x吨	(200-x)吨	200吨
B	(240-x)吨	(60+x)吨	300吨
总计	240吨	260吨	500吨

　　由题意得y_A=40x+45(200-x)=-5x+9000　 (0≤x≤200)，y_B=25(240-x)+32(60+x)=7x+7920　 (0≤x≤200)，

　　(2)若y_AB， 则-5x+9000<7x+7920，x>90.

　　∴当90≤200时， y_AB，即A村的运费较少.

　　(3)设两村运费之和为y，则y=y_A+y_B，

　　∴y=-5x+9000+7x+7920，即y=2x+16920.

　　又∵0≤x≤200时，y随x的增大而增大.

　　∴当x=0时，y有最小值，y_最小值=16920(元).

　　因此，由A村调往C仓库的香梨为0吨，调往D仓库为200吨，B村调往C仓库为240吨，调往D仓库60吨时，两村的运费之和最小，最小费用为16920元.

www.170xue.com

4.4 确定一次函数的表达式

　　专题　利用数形求一次函数的表达式

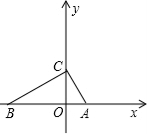
　　1.如图，在△ABC中，∠ACB=90°，AC=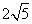，斜边AB在x轴上，点C在y轴的正半轴上，点A的坐标为（2，0）．则直角边BC所在直线的表达式为____________.

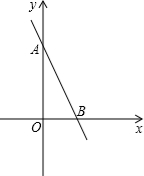
　　2. 如图，已知一条直线经过A（0，4）、点B（2，0），将这直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D，使DB=DC．求直线CD的函数表达式．

　　3.平面直角坐标系中，点A的坐标是（4，0），点P在直线y=-x+m上，且AP=OP=4．求m的值．

　　答案：

　　1.y=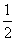x+4 【解析】 点A的坐标为（2，0），则OA=2，又A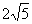C=，OC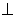AO，所以OC=4，即C（0，4）.在△ABC中，∠ACB=90°，AC=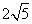，OC⊥AB与O，则AB=10，则OB=8，因而B的坐标是（-8，0），直线BC的表达式是y=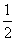x+4．

　　2．解：设直线AB的表达式为y=kx+b，把A（0，4）、点B（2，0）代入得k=-2，b=4，故直线AB的表达式为y=-2x+4.将这直线向左平移与x轴负半轴、y轴负半轴分别交于点C、点D，使DB=DC时，因为平移后的图形与原图形平行，故平移以后的函数表达式为：y=-2x-4．

　　3．解：由已知AP=OP，点P在线段OA的垂直平分线PM上，M为垂足．

　　　∵A(4，0)，∴OA=AP=OP=4，

　　　∴△AOP是等边三角形．

　　　如图，当点P在第一象限时，OM=2，OP=4．

　　　在Rt△OPM中，PM=，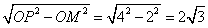

　　　∴P（2，

上一页  [1] [2] [3] [4]  下一页

，初二上册一次函数练习题及答案