12-20 22:59:40 浏览次数:823次 栏目:初二数学试题
第三章 位置与坐标
3.2平面直角坐标系
专题一 与平面直角坐标系有关的规律探究题
1.如图,在平面直角坐标系中,有若干个整数点(横纵坐标都为整数的点),其顺序按图中“→”方向排列,如:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),(4,0),(4,1),…,观察规律可得,该排列中第100个点的坐标是( ).
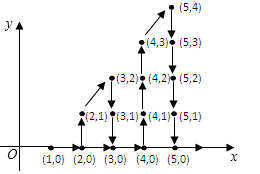
A.(10,6) B.(12,8) C.(14,6) D.(14,8)
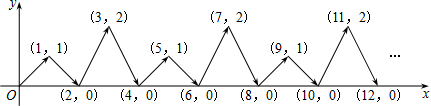
2.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2013次运动后,动点P的坐标是_____________.
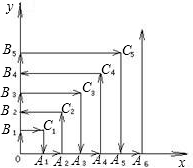
3.如图,一粒子在区域直角坐标系内运动,在第1秒内它从原点运动到点B1(0,1),接着由点B1→C1→A1,然后按图中箭头所示方向在x轴,y轴及其平行线上运动,且每秒移动1个单位长度,求该粒子从原点运动到点P(16,44)时所需要的时间.
专题二 坐标与图形
4.如图所示,A(-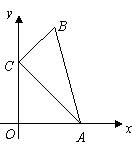 ,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )
,0)、B(0,1)分别为x轴、y轴上的点,△ABC为等边三角形,点P(3,a)在第一象限内,且满足2S△ABP=S△ABC,则a的值为( )
A. B.
B.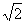 C.
C. D.2
D.2
5.如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),如果要使△ABD与△ABC全等,那么点D的坐标是____________________________________.
6.如图,在直角坐标系中,△ABC满足,∠C=90°,AC=4,BC=2,点A、C分别在x轴、y轴上,当A点从原点开始在x轴正半轴上运动时,点C随着在y轴正半轴上运动.
(1)当A点在原点时,求原点O到点B的距离OB;
(2)当OA=OC时,求原点O到点B的距离OB.

答案:
1.D 【解析】因为1+2+3+…+13=91,所以第91个点的坐标为(13,0).因为在第14行点的走向为向上,故第100个点在此行上,横坐标就为14,纵坐标为从第92个点向上数8个点,即为8.故第100个点的坐标为(14,8).故选D.
2.D 【解析】根据动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),∴第4次运动到点(4,0),第5次接着运动到点(5,1),…,∴横坐标为运动次数,经过第2013次运动后,动点P的横坐标为2013,纵坐标为1,0,2,0,每4次一轮,∴经过第2013次运动后,动点P的纵坐标为:2013÷4=503余1,故纵坐标为四个数中第一个,即为1,∴经过第2013次运动后,动点P的坐标是:(2013,2),故答案为:(2013,1).
3.解:设粒子从原点到达An、Bn、Cn时所用的时间分别为an、bn、cn,
则有:a1=3,a2=a1+1,a3=a1+12=a1+3×4,a4=a3+1,a5=a3+20=a3+5×4,a6=a5+1,…,a2n-1=a2n-3+(2n-1)×4,a2n=a2n-1+1,
∴a2n-1=a1+4[3+5+…+(2n-1)]=4n2-1,a2n=a2n-1+1=4n2,
∴b2n-1=a2n-1-2(2n-1)=4n2-4n+1,b2n=a2n+2×2n=4n2+4n,
c2n-1=b2n-1+(2n-1)=4n2-2n=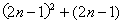 ,c2n=a2n+2n=4n2+2n=(2n)2+2n,
,c2n=a2n+2n=4n2+2n=(2n)2+2n,
∴cn=n2+n,
∴粒子到达(16,44)所需时间是到达点C44时所用的时间,再加上44-16=28(s),所以t=442+447+28=2008(s).
www.170xue.com4.C【解析】过P点作PD⊥x轴,垂足为D,
由A(﹣
 ,0)、B(0,1),得OA=
,0)、B(0,1),得OA= ,OB=1,由勾股定理,得AB=
,OB=1,由勾股定理,得AB=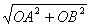 =2,
=2,
∴S△ABC=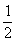 ×2×
×2×
tag: 练习题 初二数学试题,八年级数学试题,初中数学学习方法,初中学习 - 初二学习 - 初二数学 - 初二数学试题
相关分类
初二数学试题 推荐