12-20 22:53:02 浏览次数:636次 栏目:高考数学复习
2013高考数学复习:直线和圆的方程(二)
【知识图解】

【方法点拨】
1.掌握直线的倾斜角,斜率以及直线方程的各种形式,能正确地判断两直线位置关系,并能熟练地利用距离公式解决有关问题.注意直线方程各种形式应用的条件.了解二元一次不等式表示的平面区域,能解决一些简单的线性规划问题.
2.掌握关于点对称及关于直线对称的问题讨论方法,并能够熟练运用对称性来解决问题.
3.熟练运用待定系数法求圆的方程.
4.处理解析几何问题时,主要表现在两个方面:(1)根据图形的性质,建立与之等价的代数结构;(2)根据方程的代数特征洞察并揭示图形的性质.
5.要重视坐标法,学会如何借助于坐标系,用代数方法研究几何问题,体会这种方法所体现的数形结合思想.
6.要善于综合运用初中几何有关直线和圆的知识解决本章问题;还要注意综合运用三角函数、平面向量等与本章内容关系比较密切的知识.
第2课 两条直线的位置关系
【考点导读】
1.掌握两条直线平行与垂直的条件,能根据直线方程判定两条直线的位置关系,会求两条相交直线的交点,掌握点到直线的距离公式及两平行线间距离公式.
2.高考数学卷重点考察两直线平行与垂直的判定和点到直线的距离公式的运用,有时考察单一知识点,有时也和函数三角不等式等结合,题目难度中等偏易.
【基础练习】
1.已知过点A(-2,m)和B(m,4)的直线与直线2x+y-1=0平行,则m的值为-8
2.过点(-1,3)且垂直于直线x-2y+3=0的直线方程为2x+y-1=0
3.若三条直线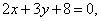
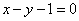 和
和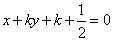 相交于一点,则k的值等于
相交于一点,则k的值等于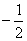 .
.
 【范例导析】
【范例导析】
例1.已知两条直线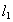 :x+m2y+6=0,
:x+m2y+6=0,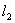 :(m-2)x+3my+2m=0,当m为何值时,
:(m-2)x+3my+2m=0,当m为何值时,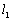 与
与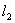
(1) 相交;(2)平行;(3)重合?
分析:利用垂直、平行的充要条件解决.
解:当m=0时,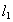 :x+6=0,
:x+6=0,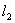 :x=0,∴
:x=0,∴ ∥
∥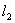 ,
,
当m=2时,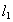 :x+4y+6=0,
:x+4y+6=0,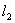 :3y+2=0
:3y+2=0
∴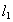 与
与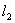 相交;
相交;
当m≠0且m≠2时,由 得m=-1或m=3,由
得m=-1或m=3,由 得m=3
得m=3
故(1)当m≠-1且m≠3且m≠0时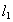 与
与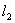 相交。
相交。
(2)m=-1或m=0时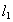 ∥
∥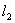 ,
,
(3)当m=3时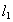
tag: 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐