12-20 22:53:02 浏览次数:791次 栏目:高考数学复习
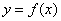 的图像关于原点对称;
的图像关于原点对称;
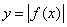 保留
保留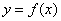 的图像在x轴上方的部分,将x轴下方的部分关于x轴翻折上去,并去掉原下方的部分;
的图像在x轴上方的部分,将x轴下方的部分关于x轴翻折上去,并去掉原下方的部分;
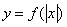 将
将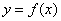 的图像在y轴右边的部分沿y轴翻折到y轴的左边部分替代原y轴左边部分,并保留
的图像在y轴右边的部分沿y轴翻折到y轴的左边部分替代原y轴左边部分,并保留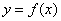 在y轴右边部分.
在y轴右边部分.
例2.设函数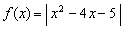 .
.
(1)在区间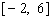 上画出函数
上画出函数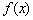 的图像;
的图像;
(2)设集合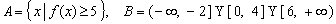 . 试判断集合
. 试判断集合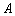 和
和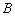 之间的关系,并给出证明.
之间的关系,并给出证明.

分析:根据图像变换得到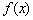 的图像,第(3)问实质是恒成立问题.
的图像,第(3)问实质是恒成立问题.
 解:(1)
解:(1)
(2)方程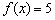 的解分别是
的解分别是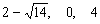 和
和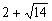 ,由于
,由于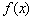 在
在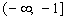 和
和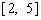 上单调递减,在
上单调递减,在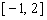 和
和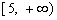 上单调递增,因此
上单调递增,因此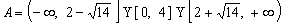 .
.
由于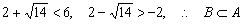 .
.
【反馈演练】
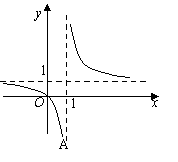
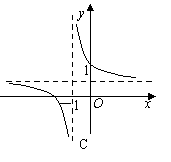
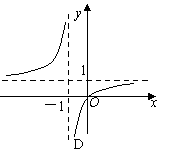
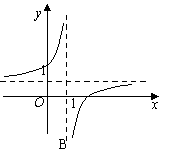
1.函数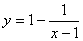 的图象是(B )
的图象是(B )
2.为了得到函数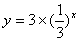 的图象,可以把函数
的图象,可以把函数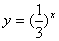 的图象向右平移1个单位长度得到.
的图象向右平移1个单位长度得到.
3.已知函数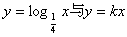 的图象有公共点A,且点A的横坐标为2,则
的图象有公共点A,且点A的横坐标为2,则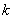
tag: 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐