12-20 22:58:55 浏览次数:569次 栏目:高考数学复习
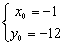
∴切点为(1,-8)或(-1,-12)
切线方程为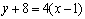 或
或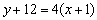 即
即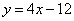 或
或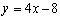
点评:函数导数的几何意义揭示了导数知识与平面解析几何知识的密切联系,利用导数能解决许多曲线的切线问题,其中寻找切点是很关键的地方。
变题:求曲线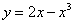 的过点
的过点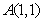 的切线方程。
的切线方程。
答案: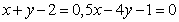
点评:本题中“过点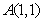 的切线”与“在点
的切线”与“在点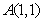 的切线”的含义是不同的,后者是以
的切线”的含义是不同的,后者是以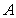 为切点,只有一条切线,而前者不一定以
为切点,只有一条切线,而前者不一定以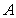 为切点,切线也不一定只有一条,所以要先设切点,然后求出切点坐标,再解决问题。
为切点,切线也不一定只有一条,所以要先设切点,然后求出切点坐标,再解决问题。
【反馈演练】
1.一物体做直线运动的方程为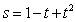 ,
,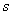 的单位是
的单位是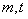 的单位是
的单位是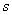 ,该物体在3秒末的瞬时速度是
,该物体在3秒末的瞬时速度是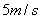 。
。
2.设生产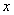 个单位产品的总成本函数是
个单位产品的总成本函数是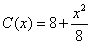 ,则生产8个单位产品时,边际成本是 2 。
,则生产8个单位产品时,边际成本是 2 。
3.已知函数f(x)在x=1处的导数为3,则f(x)的解析式可能为 (1) 。
(1)f(x)=(x-1)2+3(x-1) (2)f(x)=2(x-1)
(3)f(x)=2(x-1)2 (4)f(x)=x-1
4.若曲线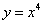 的一条切线
的一条切线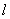 与直线
与直线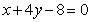 垂直,则
垂直,则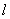 的方程为
的方程为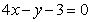 。
。
5.在函数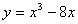 的图象上,其切线的倾斜角小于
的图象上,其切线的倾斜角小于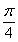 的点中,坐标为整数的点的个数是 3 。
的点中,坐标为整数的点的个数是 3 。
6.过点(0,-4)与曲线y=x3+x-2相切的直线方程是 y=4x-4 .
7. 求下列函数的导数:
(1)y=(2x2-1)(3x+1) (2)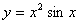 (3)
(3)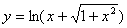
(4)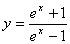
tag: 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐