12-20 22:58:55 浏览次数:569次 栏目：高考数学复习
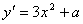和
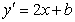，且在点P处有公切数
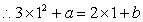，得b=2
又由
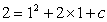，得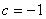
【范例导析】
例1．下列函数的导数：
①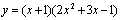
②
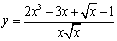③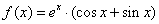
分析：利用导数的四则运算求导数。
解：①法一：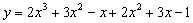
∴ 
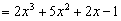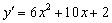
法二：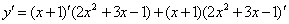
=
+
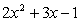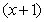
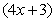
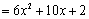
②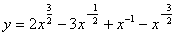 
∴ 
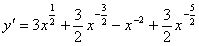
③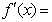
e－x（cosx+sinx）+e－x（－sinx+cosx）
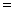2e－xcosx，
点评：利用基本函数的导数、导数的运算法则及复合函数的求导法则进行导数运算，是高考对导数考查的基本要求。
例2． 如果曲线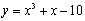
的某一切线与直线
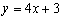平行，求切点坐标与切线方程．
分析：本题重在理解导数的几何意义：曲线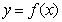
在给定点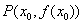
处的切线的斜率
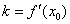，用导数的几何意义求曲线的斜率就很简单了。
解：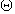
切线与直线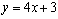
平行， 斜率为4
又切线在点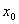
的斜率为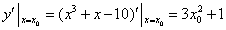
∵ 
∴
∴
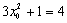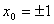
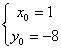
tag: 高考数学 高考数学复习，高考数学复习大全,高考复习方法，高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐
