12-20 22:58:55 浏览次数:668次 栏目:高考数学复习
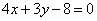 距离的最小值是
距离的最小值是
5.若直线l过抛物线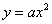 (a>0)的焦点,并且与y轴垂直,若l被抛物线截得的线段长为4,则a=
(a>0)的焦点,并且与y轴垂直,若l被抛物线截得的线段长为4,则a=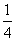
6.某抛物线形拱桥跨度是20米,拱高4米,在建桥时每隔4米需用一支柱支撑,求其中最长的支柱的长.
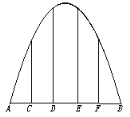
解:以拱顶为原点,水平线为x轴,建立坐标系,
如图,由题意知,|AB|=20,|OM|=4,A、B坐标分别为(-10,-4)、(10,-4)
设抛物线方程为x2=-2py,将A点坐标代入,得100=-2p×(-4),解得p=12.5,
于是抛物线方程为x2=-25y.
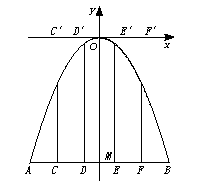

由题意知E点坐标为(2,-4),E′点横坐标也为2,将2代入得y=-0.16,从而|EE′|=
(-0.16)-(-4)=3.84.故最长支柱长应为3.84米.
7.已知抛物线的顶点在原点,焦点F在x轴的正半轴,且过点P(2,2),过F的直线交抛物线于A,B两点.(1)求抛物线的方程;
(2)设直线l是抛物线的准线,求证:以AB为直径的圆与直线l相切.
分析:可设抛物线方程为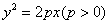 .用待定系数法求得方程,对于第二问的证明只须证明
.用待定系数法求得方程,对于第二问的证明只须证明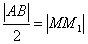 ,则以AB为直径的圆,必与抛物线准线相切.
,则以AB为直径的圆,必与抛物线准线相切.
解:(1)设抛物线的方程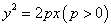 ,将(2,2)代入得
,将(2,2)代入得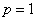 ∴所求抛物线方程为
∴所求抛物线方程为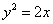
 (2)证明:作
(2)证明:作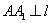 于
于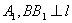 于
于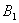 .M为AB中点,作
.M为AB中点,作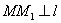 于
于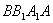 ,则由抛物线的定义可知:
,则由抛物线的定义可知: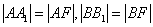
在直角梯形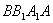 中:
中:
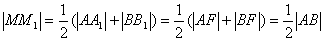
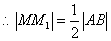 ,故以AB为直径的圆,必与抛物线的准线相切.
,故以AB为直径的圆,必与抛物线的准线相切.
点拨:类似有:以椭圆焦点弦为直径的圆与相对应的准线相离,以双曲线焦点弦为直径的圆与相应的准线相交.
,2017高考数学复习:圆锥曲线(四)tag: 圆锥曲线 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐