12-20 22:58:55 浏览次数:757次 栏目:高考数学复习
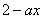 在
在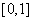 上要大于零,即
上要大于零,即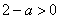 ,即
,即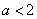 ;综上,
;综上,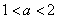 .
.
(2)①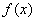 有无最小值与a的取值有关;②当
有无最小值与a的取值有关;②当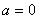 时,
时,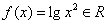 ,成立;
,成立;
③当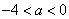 时,若
时,若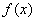 的定义域为
的定义域为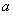 ,则
,则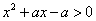 恒成立,即
恒成立,即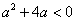 ,即
,即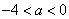 成立;④若
成立;④若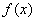 在区间
在区间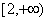 上单调递增,则
上单调递增,则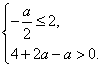 解得
解得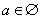 ,不成立.
,不成立.
点评:解决对数函数有关问题首先要考虑定义域,并能结合对数函数图像分析解决.
例3.已知函数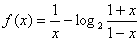 ,求函数
,求函数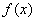 的定义域,并讨论它的奇偶性和单调性.
的定义域,并讨论它的奇偶性和单调性.
分析:利用定义证明复合函数的单调性.
解:x须满足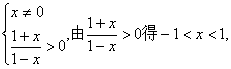 所以函数
所以函数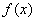 的定义域为(-1,0)∪(0,1).
的定义域为(-1,0)∪(0,1).
因为函数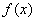 的定义域关于原点对称,且对定义域内的任意x,有
的定义域关于原点对称,且对定义域内的任意x,有
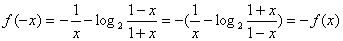 ,所以
,所以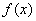 是奇函数.
是奇函数.
研究
点评:本题重点考察复合函数单调性的判断及证明,运用函数性质解决问题的能力.
【反馈演练】
1.给出下列四个数:①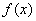 在(0,1)内的单调性,任取x1、x2∈(0,1),且设x1
在(0,1)内的单调性,任取x1、x2∈(0,1),且设x1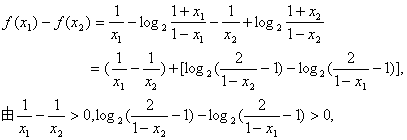 得
得 >0,即
>0,即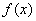 在(0,1)内单调递减,由于
在(0,1)内单调递减,由于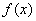 是奇函数,所以
是奇函数,所以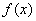 在(-1,0)内单调递减.
在(-1,0)内单调递减.
 ;②
;②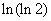 ;③
;③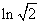 ;④
;④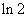
tag: 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐