12-20 22:52:45 浏览次数:837次 栏目:高考备考
包含a的有5个,所以,P(A)= , 答: a能获一等奖的概率为
, 答: a能获一等奖的概率为 . ……………………………………6分
. ……………………………………6分
(Ⅱ)设“若a、b已获一等奖,c能获奖”为事件B,
a、b已获一等奖,余下的四个人中,获奖的基本事件有(c,c)、(c、d)、(c、e)、(c、f)、(d,c)、(d、d)、(d、e)、(d、f)、(e,c)、(e、d)、(e、e)、(e、f)、(f,c)、(f、d)、(f、e)、(f、f)16个, …………………………………………………………………………………………11分
其中含有c的有7种,所以,P(B)= ,
,
答:若a、b已获一等奖,c能获奖的概率为 . …………………………………………………13分
. …………………………………………………13分
18.(本题14分) 已知函数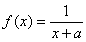 ,
, .
.
(1)设函数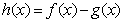 ,且
,且 求a,b的值;
求a,b的值;
(2)当a=2且b=4时,求函数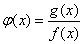 的单调区间,并讨论该函数在区间(-2,m](
的单调区间,并讨论该函数在区间(-2,m](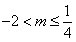 )上的最大值。
)上的最大值。
解:(Ⅰ)函数h(x)定义域为{x|x≠-a},……………………………………………………………1分
则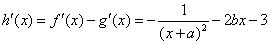 ,………………………………………………………3分
,………………………………………………………3分
因为 所以
所以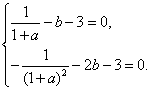 解得,
解得, 或
或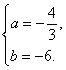 ……………………6分
……………………6分
(Ⅱ)记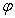 (x)=
(x)= ,则
,则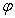 (x)=(x+a)(bx2+3x)(x≠-a) ,
(x)=(x+a)(bx2+3x)(x≠-a) ,
 因为a=2,b=4,所以
因为a=2,b=4,所以 (x≠-2), ………………………………………7分
(x≠-2), ………………………………………7分
 ,
,
令 ,得
,得 ,或
,或 , ……………………………………………………………8分
, ……………………………………………………………8分
当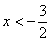
相关分类
高考备考 推荐