12-20 22:52:45 浏览次数:837次 栏目:高考备考
2013北京丰台区高考文科数学一模练习答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | A | D | B | A | D | B | C | C |
二.填空题
9.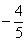 ; 10. 30 ; 11.
; 10. 30 ; 11. 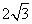 ; 12. 2 ; 13. -1 ; 14.
; 12. 2 ; 13. -1 ; 14. 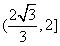 .
.
三.解答题
15. (本题13分)已知函数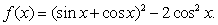
(Ⅰ)求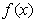 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ)求函数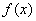 在
在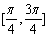 上的值域.
上的值域.
解:(Ⅰ) , …………………………………3分
, …………………………………3分
 最小正周期T=
最小正周期T=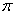 , ……………..………………………………………………………………4分
, ……………..………………………………………………………………4分
单调增区间 , ………………………………………………………7分
, ………………………………………………………7分
(Ⅱ)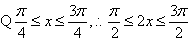 ,
,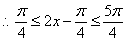 , ……………………………10分
, ……………………………10分

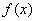 在
在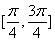 上的值域是
上的值域是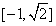 . ……………………………………………………13分
. ……………………………………………………13分
16. (本题13分)如图,四棱锥P-ABCD中, BC∥AD,BC=1,AD=3,AC⊥CD,且平面PCD⊥平面ABCD.
(Ⅰ)求证:AC⊥PD;
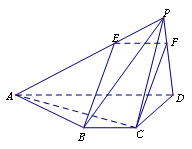
(Ⅱ)在线段PA上,是否存在点E,使BE∥平面PCD?若存在,求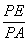 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
解:(Ⅰ)∵平面PCD⊥平面ABCD,平面PCD∩平面ABCD=CD,AC⊥CD, AC⊂平面ABCD,
∴AC⊥平面PCD, ...........................4分
∵PD⊂平面PCD,
∴AC⊥PD. .................................6分
(Ⅱ)线段PA上,存在点E,使BE∥平面PCD, ......7分
∵AD=3,
∴在△PAD中,存在EF//AD(E,F分别在AP,PD上),且使EF=1,
又∵ BC∥AD,∴BC∥EF,且BC=EF,
∴四边形BCFE是平行四边形, ...................................................9分
∴BE//CF, 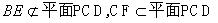 ,
,
∴BE∥平面PCD, ..............................................................11分
∵EF=1,AD=3,
∴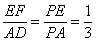 . ..............................................................13分
. ..............................................................13分
17.(本题13分)在一次抽奖活动中,有a、b、c、d、e、f 共6人获得抽奖的机会。抽奖规则如下:主办方先从6人中随机抽取两人均获一等奖,再从余下的4人中随机抽取1人获二等奖,最后还从这4人中随机抽取1人获三等奖。
(Ⅰ)求a能获一等奖的概率;
(Ⅱ)若a、b已获一等奖,求c能获奖的概率。
解:(Ⅰ)设“a能获一等奖”为事件A,
,2017北京丰台区高考文科数学一模练习答案相关分类
高考备考 推荐