12-20 22:52:45 浏览次数:773次 栏目:高考备考
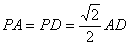 ,若E,F分别为PC,BD的中点.
,若E,F分别为PC,BD的中点.
(1)求证: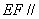 平面PAD;
平面PAD;
(2)求证:平面PDC 平面PAD;
平面PAD;
(3)求四棱锥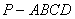 的体积.
的体积.
21.(本小题满分12分)
已知椭圆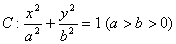 过点
过点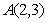 ,且离心率
,且离心率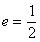 .
.
(1)求椭 圆
圆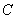 的标准方程;
的标准方程;
(2)是否存在过点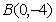 的直线
的直线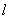 交椭圆于不同的两点M、N,且满足
交椭圆于不同的两点M、N,且满足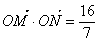 (其中点O为坐标原点),若存在,求出直线
(其中点O为坐标原点),若存在,求出直线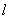 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
22.(本小题满分14分)
已知函数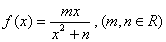 在
在 处取得极小值2.
处取得极小值2.
(1)求函数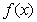 的解析式;
的解析式;
(2)求函数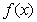 的极值;
的极值;
(3)设函数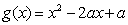 ,若对于任意
,若对于任意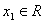 ,总存在
,总存在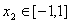 ,使得
,使得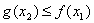 ,求实数
,求实数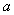 的取值范围.
的取值范围.
参考答案:

又当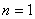 时,
时,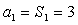 ,满足上式 ……4分
,满足上式 ……4分
∴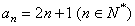 ……5分
……5分
(2)由(1)可知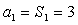 ,
,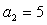 ,
,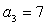 ……7分
……7分
又
∴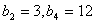 ……8分
……8分
又数列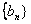 是公比为正数等比数列
是公比为正数等比数列
相关分类
高考备考 推荐