12-20 22:52:45 浏览次数:707次 栏目:高考备考
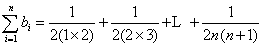
=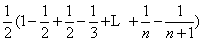 =
= .….……………..…………10分
.….……………..…………10分
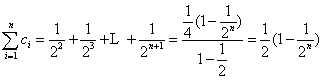 . ……………………….11分
. ……………………….11分
(方法一)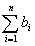 -
-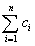 =
=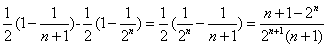 .
.
当n=1时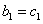 不符合题意,
不符合题意,
当n=2时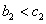 ,符合题意,
,符合题意,
猜想对于一切大于或等于2的自然数,都有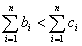 .(
.(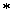 )
)
观察知,欲证(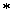 )式,只需证明当n≥2时,n+1<2n
)式,只需证明当n≥2时,n+1<2n
以下用数学归纳法证明如下:
(1)当n=2时,左边=3,右边=4,左边<右边;
(2)假设n=k(k≥2)时,(k+1)<2k,
当n=k+1时,左边=(k+1)+1<2k+1<2k+2k=2k+1=右边,
 对于一切大于或等于2的正整数,都有n+1<2n,即
对于一切大于或等于2的正整数,都有n+1<2n,即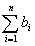 <
<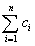 成立.
成立.
综上,满足题意的n的最小值为2. ……………………………………………..13分
(方法二)欲证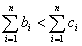 成立,只需证明当n≥2时,n+1<2n.
成立,只需证明当n≥2时,n+1<2n.
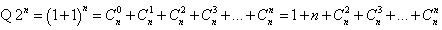 ,
,
并且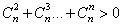 ,
,
 当
当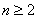 时,
时,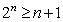 .
.
相关分类
高考备考 推荐