12-20 22:58:55 浏览次数:465次 栏目:高考备考
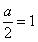 ,即
,即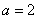 时,
时,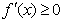 恒成立,函数
恒成立,函数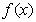 的单调递增区间为
的单调递增区间为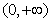 . …7分
. …7分
(Ⅱ)①当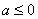 时,由(Ⅰ)可知,函数
时,由(Ⅰ)可知,函数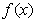 的单调递减区间为
的单调递减区间为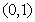 ,
,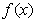 在
在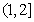 单调递增.
单调递增.
所以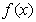 在
在 上的最小值为
上的最小值为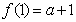 ,
,
由于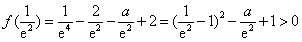 ,
,
要使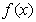 在
在 上有且只有一个零点,需满足
上有且只有一个零点,需满足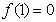 或
或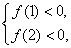 解得
解得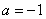 或
或 .
.
②当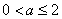 时,由(Ⅰ)可知,
时,由(Ⅰ)可知,
(ⅰ)当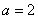 时,函数
时,函数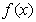 在
在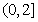 上单调递增;
上单调递增;
且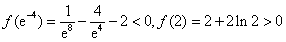 ,所以
,所以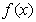 在
在 上有且只有一个零点.
上有且只有一个零点.
(ⅱ)当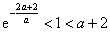 时,函数
时,函数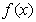 在
在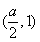 上单调递减,在
上单调递减,在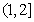 上单调递增;
上单调递增;
又因为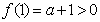 ,所以当
,所以当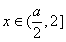 时,总有
时,总有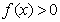 .
.
因为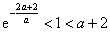
相关分类
高考备考 推荐