12-20 22:58:55 浏览次数:812次 栏目:高考备考
因为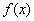 是二阶比增函数,即
是二阶比增函数,即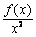 是增函数.
是增函数.
所以当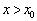 时,
时,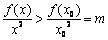 ,所以
,所以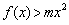
所以一定可以找到一个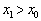 ,使得
,使得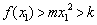
这与 对
对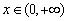 成立矛盾 ………………11分
成立矛盾 ………………11分
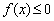 对
对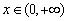 成立
成立
所以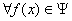 ,
,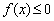 对
对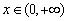 成立
成立
下面我们证明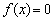 在
在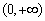 上无解
上无解
假设存在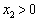 ,使得
,使得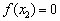 ,
,
则因为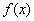 是二阶增函数,即
是二阶增函数,即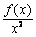 是增函数
是增函数
一定存在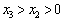 ,
,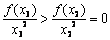 ,这与上面证明的结果矛盾
,这与上面证明的结果矛盾
所以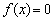 在
在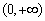 上无解
上无解
综上,我们得到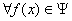 ,
,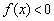 对
对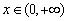 成立
成立
所以存在常数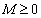 ,使得
,使得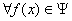 ,
,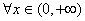 ,有
,有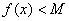 成立
成立
又令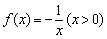 ,则
,则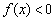 对
对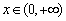 成立,
成立,
又有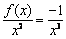 在
在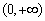
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] 下一页
,海淀区高三上册数学理科试卷及答案相关分类
高考备考 推荐