12-20 22:59:14 浏览次数:869次 栏目:高二数学试题
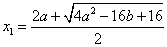 ,
, ………9分
………9分
∴
又∵点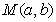 在抛物线
在抛物线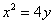 上,∴
上,∴ ,………10分
,………10分
∴ 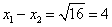 ,即
,即 =4---------------------------------13分
=4---------------------------------13分
∴当 运动时,弦长
运动时,弦长 为定值4…………………………………………………14分
为定值4…………………………………………………14分
〔方法2:∵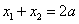 ,
,
∴


又∵点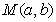 在抛物线
在抛物线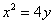 上,∴
上,∴ , ∴
, ∴ 

∴当 运动时,弦长
运动时,弦长 为定值4〕
为定值4〕
20.证明:①必要性:
a1=S1=p+q. …………1分
当n≥2时,an=Sn-Sn-1=pn-1(p-1)
∵p≠0,p≠1,∴ =p…………3分
=p…………3分
若{an}为等比数列,则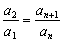 =p ∴
=p ∴ =p,…………5分
=p,…………5分
∵p≠0,∴p-1=p+q,∴q=-1…………6分
②充分性
当q=-1时,∴Sn=pn-1(p≠0,p≠1),a1=S1=p-1…………7分
当n≥2时,an=Sn-Sn-1=pn-pn-1=pn-1(p-1)
∴an=(p-1)pn-1 (p≠0,p≠1) …………9分
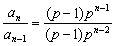 =p为常数…………11分
=p为常数…………11分
∴q=-1时,数列{an}为等比数列.即数列{an}是等比数列的充要条件为q=-1.…12分
21.解:(1)设动圆圆心为 ,半径为
,半径为 .
.
由题意,得 ,
,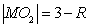 ,
, . …………3分
. …………3分
 由椭圆定义知
由椭圆定义知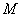 在以
在以 为焦点的椭圆上,且
为焦点的椭圆上,且 ,
,

 动圆圆心M的轨迹
动圆圆心M的轨迹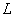 的方程为
的方程为 .
. ……6分
……6分
(2) 设 、
、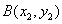 (
( ),
),
则 , ……8分
, ……8分
由 ,得
,得 ,
,
解得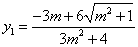 ,
, , …………10分
, …………10分
∴ ,令
,令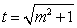 ,则
,则 ,且
,且 ,
,
有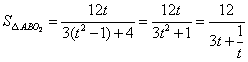 ,令
,令 ,
,



 在
在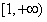 上单调递增,有
上单调递增,有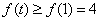 ,
, ,
,
此时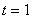 ,
, ∴存在直线
∴存在直线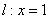 ,
, 的面积最大值为3. …………14分
的面积最大值为3. …………14分
tag: 数学 实验中学 广东 高二数学试题,高二数学试题大全,高二学习方法,高中学习 - 高二学习 - 高二数学 - 高二数学试题
相关分类
高二数学试题 推荐