12-20 22:59:40 浏览次数:853次 栏目:初二数学试题
期末测试题
【本试卷满分120分,测试时间120分钟】
一、选择题(每小题3分,共36分)
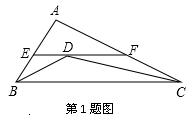
1.如图,在△ABC中,BD、CD分别平分∠ABC、∠ACB,过点D作直线平行于BC,分别交AB、AC于点E、F,当∠A的位置及大小变化时,线段EF和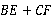 的大小关系是( )
的大小关系是( )
A.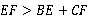 B.
B.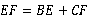 C.
C.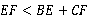 D.不能确定
D.不能确定
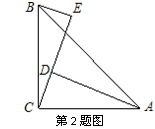
2.如图,已知∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于点D,AD=2.5cm,DE=1.7cm,则BE=( )
A.1cm B.0.8cm C.4.2cm D.1.5cm
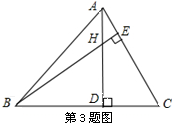
3.如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为( )
A.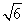 B.
B.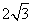 C.5 D.4
C.5 D.4
4.已知一次函数y=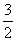
 +m和y=
+m和y=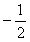
 +n的图象都经过点A(-2,0),且与y轴分别交于B、C两点,那么△ABC的面积是( )
+n的图象都经过点A(-2,0),且与y轴分别交于B、C两点,那么△ABC的面积是( )
A.2 B.3 C.4 D.6
5.若点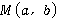 在第四象限,则点
在第四象限,则点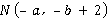 在( )
在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.已知一次函数 的图象经过第一、二、三象限,则b的值可以是( )
的图象经过第一、二、三象限,则b的值可以是( )
A.-1 B.0 C. 2 D.任意实数
7.俄罗斯方块游戏中,若某行被小方格块填满,则该行中的所有小方格会自动消失.现在游戏机屏幕下面三行已拼成如图所示的图案,屏幕上方又出现一小方格块正向下运动,为了使屏幕下面三行中的小方格都自动消失,你可以进行以下哪项操作( )
A.先逆时针旋转90°,再向左平移 B.先顺时针旋转90°,再向左平移
C.先逆时针旋转90°,再向右平移 D.先顺时针旋转90?,再向右平移

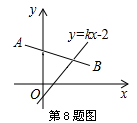
8.如图,在平面直角坐标系中,线段AB的端点坐标为A(-2,4), B(4,2),直线
B(4,2),直线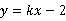 与线段AB有交点,则k的值不可能是( )
与线段AB有交点,则k的值不可能是( )
A.-5 B.-2 C.3 D. 5
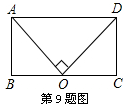
9.如图,在矩形ABCD中,O是BC的中点,∠AOD= 90°,若矩形ABCD的周长为30cm,则AB的长为( )
A.5 cm B.10 cm C.15 cm D.7.5 cm
10.下列说法正确的是( )
A.数据3,4,4,7,3的众数是4
B.数据0,1,2,5,a的中位数是2
C.一组数据的众数和中位数不可能相等
D.数据0,5,-7,-5,7的中位数和平均数都是0
11.张强有图书40册,李锋有图书30册,他们又从图书馆借了22本图书后,每人的图书册数相同,则张强借了( ) 
A.5本 B.6本 C.7本 D.8本
12.(2011•泸州中考)小明的父亲饭后出去散步,从家中出发走20分钟到一个离家900米的报亭看报10分钟后,用15分钟返回家,下列图中表示小明的父亲离家的距离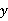 (米)与离家的时间
(米)与离家的时间 (分)之间的函数关系的是( )
(分)之间的函数关系的是( )

二、填空题(每小题3分,共30分)
13.如图,△ABC中,AB=AC,BD是角平分线,BE=BD,∠A=72°,则∠DEC= _______.
14.某市为鼓励居民节约用水,对自来水用户收费办法调整为:若每户每月不超过12吨,则每吨收取a元;若每户每月超过12吨,超出部分按每吨 2a元收取.若小亮家5月份缴纳水费20a元,则小亮家这个月实际用水 吨.
2a元收取.若小亮家5月份缴纳水费20a元,则小亮家这个月实际用水 吨.

15.如图,折叠矩形纸片ABCD,先折出折痕BD,再折叠使AD边与对角线BD重合,得折痕DG,若AB=4,BC=3,则AG的长是__________.
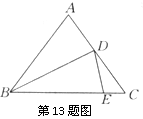
16.如图,已知四边形ABCD是菱形,∠A=72°,将它分割成如图所示的四个等腰三角形,那么∠1+∠2+∠3= .
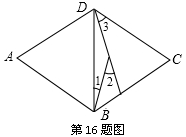
17.如图,将一朵小花放置在平面直角坐标系中第三象限内的甲位置,先将它绕原点O旋转180°到乙位置,再将它向下平移2个单位长度到丙位置,则小花顶点A在丙位置中的对应点A′的坐标为________.
18.若一组数据15,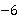 ,11,
,11, ,7的平均数为6,则
,7的平均数为6,则 的值是 .
的值是 .
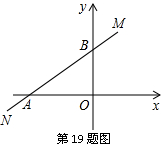
19.如图,已知直线MN: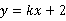 交
交 轴负半轴于点A,交
轴负半轴于点A,交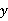 轴于点B,∠BAO=30°,点C是
轴于点B,∠BAO=30°,点C是 轴上的一点,且OC=2,则∠MBC的度数为___________.
轴上的一点,且OC=2,则∠MBC的度数为___________.
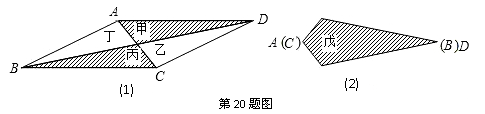
20.如图(1),平行四边形纸片ABCD的面积为120,AD=20,AB=18.沿两条对角线将四边形ABCD剪成甲、乙、 丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成对称图形戊,如图(2)所示,则图形戊的两条对角线长度之和是 .
丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成对称图形戊,如图(2)所示,则图形戊的两条对角线长度之和是 .
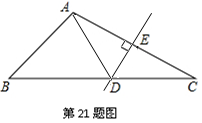
21.如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为_________cm.
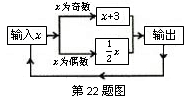
22.(2011•遵义中考)有一数值转换器,原理如图所示,若开始输入 的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2 011次输出的结果是 .
的值是5,可发现第一次输出的结果是8,第二次输出的结果是4,…,请你探索第2 011次输出的结果是 .
三、解答题(共54分)
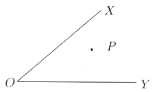 23.(6分)如图,∠XOY内有一点P,试在射线OX上找出一点M,在射线OY上找出一点N,使PM+MN+NP最短.
23.(6分)如图,∠XOY内有一点P,试在射线OX上找出一点M,在射线OY上找出一点N,使PM+MN+NP最短.
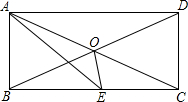 24.(6分)如图,在矩形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD交BC于点E.若∠CAE=1
24.(6分)如图,在矩形ABCD中,对角线AC、BD相交于点O,AE平分∠BAD交BC于点E.若∠CAE=1 5°,求∠BOE的度数.
5°,求∠BOE的度数.
25.(6分)在直角坐标系中,用线段顺次连接点(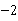 ,0),(0,3),(3,3),(4,0).
,0),(0,3),(3,3),(4,0).
(1)这是一个什么图形;
(2)求出它的面积;
(3)求出它的周长.
26.(6分)某工人上 午7点上班至11点下班,一开始他用15分钟做准备工作,接着每隔15分钟加工完1个零件.
午7点上班至11点下班,一开始他用15分钟做准备工作,接着每隔15分钟加工完1个零件.
(1)求他在上午时间内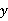 (时)与加工完零件
(时)与加工完零件 (个)之间的函数关系式.
(个)之间的函数关系式.
(2)他加工完第一个零件是几点?
(3)8点整他加工完几个零件?
(4)上午他可加工完 几个零件?
几个零件?
 27.(7分)如图,在平面直角坐标系中,函数
27.(7分)如图,在平面直角坐标系中,函数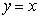 的图象
的图象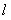 是第一、三象限的角平分线.
是第一、三象限的角平分线.
(1)实验与探究:由图观察易知A(0,2)关于直线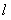 的对称点
的对称点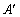 的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线
的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线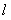 的对称点
的对称点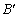 、
、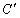 的位置,并写出它们的坐标:
的位置,并写出它们的坐标:  、
、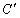 ;
;
(2)归纳与发现:结合图形观察以上三组点的坐标,
你会发现:坐标平面内任 一点P(m,n)关于第一、三象限的角平分线
一点P(m,n)关于第一、三象限的角平分线 的对称点
的对称点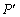 的坐标为 .
的坐标为 .
28.(7分)“种粮补贴”惠农政策的出台,大大激发了农民的种粮积极性 ,某粮食生产专业户去年计划生产小麦和玉米共18吨,实际生产了20吨,其中小麦超产12%,玉米超产10%,该专业户去年实际生产小麦、玉米各多少吨?
,某粮食生产专业户去年计划生产小麦和玉米共18吨,实际生产了20吨,其中小麦超产12%,玉米超产10%,该专业户去年实际生产小麦、玉米各多少吨?
 29.(8分)
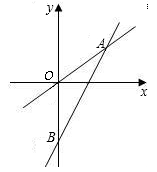
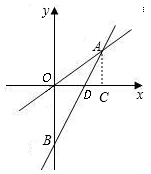
29.(8分) 如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与
如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与 轴交于点B,且OA=OB,求这两个函数的关系式及两直线与
轴交于点B,且OA=OB,求这两个函数的关系式及两直线与 轴围成的三角形的面积.
轴围成的三角形的面积.
30.(8分)某中学为了了解全校的耗电情况,抽查了10天中全校每天的耗电量,数据如下表:
| 千瓦时 | 90 | 93 | 102 | 113 | 114 | 120 |
| 天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(1)写出上表中数据的众数和平均数.
(2)根据上题获得的数据,估计该校一个月的耗电量(按30天计算).
(3)若当地每千瓦时电的价格是0.5元,写出该校应付电费y(元)与天数 (
( 取正整数,单位:天)的函数关系式.
取正整数,单位:天)的函数关系式.
参考答案:
一、选择题
1.B
解析:由BD平分∠ABC得,∠EBD=∠DBC.∵ EF∥BC,∴ ∠EDB=∠DBC,
∴ ∠EBD=∠EDB,∴ △BED是等腰三角形,∴ ED=BE.同理可得,DF=FC,
∴ EF=ED+DF=BE+FC,故选B.
2.B
解析:∵ AD⊥CE,∴ ∠E=∠ADC=90°,即∠CAD+∠ACD=90°.
∵ ∠ACB=90°,∴ ∠BCE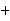 ∠ACD=90°,∴ ∠BCE=∠CAD.
∠ACD=90°,∴ ∠BCE=∠CAD.
又∵ AC=BC,∴ △BCE≌△CAD(AAS),∴ CE=AD,BE=CD.
∵ AD=2.5 cm,DE=1.7 cm,∴ 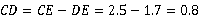 (cm),即BE=0.8 cm.
(cm),即BE=0.8 cm.
3.D
解析:∵ ∠ABC=45°,AD⊥BC,∴ AD=BD,∠ADC=∠BDH,∠AHE=∠BHD=∠C,∴ △ADC≌△BDH,∴ BH=AC=4,故选D.
4.C
解析:因为 与
与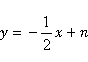 的图象都过点A(-2,0),
的图象都过点A(-2,0),
所以可得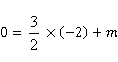 ,
,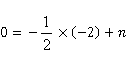 ,所以
,所以 ,
,
所以两函数表达式分别为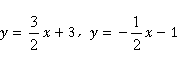 .
.
因为直线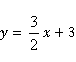 与
与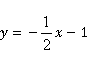 与y轴的交点分别为B(0,3),C(0,
与y轴的交点分别为B(0,3),C(0,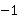 ),
),
所以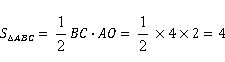 ,故选C.
,故选C.
5.B
解析:∵ 点M(a,b)在第四象限,∴ a>0,b<0,∴ 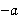 <0,
<0,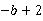 >0,
>0,
∴ 点N(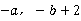 )在第二象限,故选B.
)在第二象限,故选B.
6.C
解析:∵ 一次函数的图象经过第一、二、三象限,∴ b>0,四个选项中只有C符合条件.
7.A
8.B
解析:设直线 与y轴的交点为P(0,
与y轴的交点为P(0,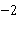 ),若它与线段AB有交点,则直线
),若它与线段AB有交点,则直线 的斜率大于等于直线PB的斜率或小于等于直线PA的斜率.可知PB的斜率为1,PA的斜率为
的斜率大于等于直线PB的斜率或小于等于直线PA的斜率.可知PB的斜率为1,PA的斜率为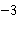 ,所以k应大于等于1或小于等于
,所以k应大于等于1或小于等于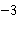 ,所以B选项不可能.
,所以B选项不可能.
9.A
解析:矩形ABCD中,O是BC的中点,∠AOD=90°,根据矩形的性质得到△ABO≌△DCO,则OA=OD,∠DAO=45°,所以∠BOA=∠BAO=45°,即BC=2AB.由矩形ABCD的周长为30 cm得到,30=2AB+2×2AB,解得AB=5 cm,故选A.
10.D
解析:数据3,4,4,7,3的众数是3和4,A错;由于不知道a的值,所以数据0,1,2,5,a的中位数不确定,B错;一组数据的众数和中位数有可能相等,C错,只有D是正确的.
11.B
解析:设张强借了 本,则李锋借了
本,则李锋借了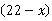 本,则
本,则 ,解得
,解得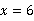 ,即张强借了6本书,故选B.
,即张强借了6本书,故选B.
12.D
解析:依题意,0~20分钟散步,离家路程增加到900米,20~30分钟看报,离家路程不变,30~45分钟返回家,离家路程减少为0米,故选D.
www.170xue.com二、填空题
13.103.5°
解析:因为AB=AC,∠A=72°,所以∠ABC=∠C=54°.因为BD是角平分线,所以∠DBC= ∠ABC= 27°.又BE=BD,所以∠BDE=∠BED=76.5°,所以∠DEC=180°
∠ABC= 27°.又BE=BD,所以∠BDE=∠BED=76.5°,所以∠DEC=180° 76.5°=103.5°.
76.5°=103.5°.
14.16
解析:设小亮家这个月实际用水 吨,则
吨,则 ,解得
,解得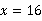 .
.
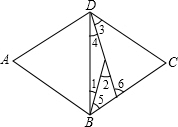 15.
15.
解析:在Rt△ABD中,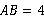 ,
, ,∴
,∴ 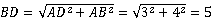 ,由折叠的性质可得,△ADG≌△A‘DG,∴
,由折叠的性质可得,△ADG≌△A‘DG,∴ 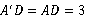 ,
, ,∴
,∴  .设
.设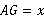 ,则
,则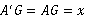 ,
,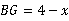 ,在Rt△A‘BG中,
,在Rt△A‘BG中,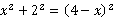 ,解得
,解得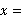
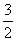 ,即
,即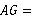
 .
.
16.90°
解析:如图,∵ 四边形ABCD是菱形,∴ ∠A=∠C=72°.
∵ ∠6=∠C=72°,∴ ∠3=180° 2×72°=36°.
2×72°=36°.
∵ ∠6=∠2+∠5=2∠2=72°,∴ ∠2=36°.
∵ ∠2=∠1+∠4=2∠1=36°,∴ ∠1=18°.
∴ ∠1+∠2+∠3=18°+36°+36°=90°.
17.(3,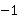 )
)
解析:由图可知A点坐标为( ,
,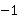 ),根据绕原点O旋转180°后横纵坐标互为相反数,∴ 旋转后得到的坐标为(3,1),根据平移“上加下减”原则,
),根据绕原点O旋转180°后横纵坐标互为相反数,∴ 旋转后得到的坐标为(3,1),根据平移“上加下减”原则,
∴ 向下平移2个单位长度得到的坐标为(3,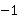 ).
).
18.3
解析:因为平均数为6,所以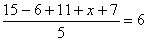 ,解得
,解得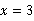 .
.
19. 165° 或75°
解析:∵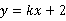 与
与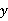 轴的交点坐标为B(0,2),∴OB=2.
轴的交点坐标为B(0,2),∴OB=2.
又∵点C是 轴上的一点,且OC=2,∴点C的坐标是(2,0)或(
轴上的一点,且OC=2,∴点C的坐标是(2,0)或(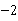 ,0).
,0).
①当C点的坐标是(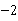 ,0)时,OB=OC=2,∴∠BCO=∠CBO=45°.
,0)时,OB=OC=2,∴∠BCO=∠CBO=45°.
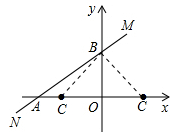 ∵∠BAO=30°,∴∠ABO=60°,∴∠ABC=60°
∵∠BAO=30°,∴∠ABO=60°,∴∠ABC=60° 45°=15°,
45°=15°,
∴∠MBC=180°-15°=165°;
②当C点的坐标是(2,0)时,OB=OC=2,∴∠BCO=∠CBO=45°.
∵∠BAO=30°,∴∠ABO=60°,∴∠MBC=180° 45°
45° 60°=75°.
60°=75°.
综合①②知,∠MBC的度数为165° 或75°.
20.26
解析:∵ AD=20,平行四边形的面积是120,∴ AD边上的高是6.
∴ 要求的两条对角线长度之和是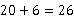 .
.
21.19
解析:∵ DE是AC的垂直平分线,∴ 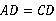 ,
,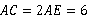 .
.
又∵ △ABD的周长 ,∴
,∴  ,
,
即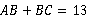 ,∴ △ABC的周长
,∴ △ABC的周长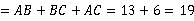 (cm).
(cm).
22.1
解析:由已知要求得出:第一次输出结果为:8,
第二次为4,第三次为2,第四次为1,那么第五次为4,…,
所以得到从第二次开始每三次一个循环,(2 011 1)÷3=670,
1)÷3=670,
所以第2 011次输出的结果是1.
三、解答题
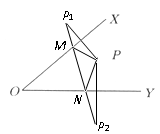 23.解:如图所示,分别以直线OX、OY为对称轴,作点P的对称点
23.解:如图所示,分别以直线OX、OY为对称轴,作点P的对称点 与
与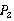
连接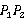 ,分别交OX于点M,交OY于点N,则PM+MN+NP最短.
,分别交OX于点M,交OY于点N,则PM+MN+NP最短.
24.解:∵AE平分∠BAD,∴∠BAE=∠EAD=45°.
又知∠EAO=15°,∴∠OAB=60°.
∵OA=OB,∴△BOA为等边三角形,∴BA=BO.
∵∠BAE=45°,∠ABC=90°,
∴△BAE为等腰直角三角形,∴BA=BE.
∴BE=BO,∠EBO=30°,∠BOE=∠BEO,此时∠BOE=75°.
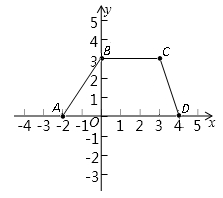 25.解:(1)因为(0,3)和(3,3)的纵坐标相同,因而BC∥AD,
25.解:(1)因为(0,3)和(3,3)的纵坐标相同,因而BC∥AD,
故四边形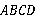 是梯形.作出图形如图所示.
是梯形.作出图形如图所示.
(2)因为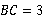 ,
,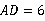 ,高
,高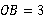 ,
,
故梯形的面积是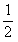
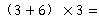
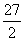 .
.
(3)在Rt△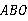 中,根据勾股定理得
中,根据勾股定理得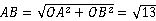 ,
,
同理可得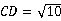 ,因而梯形的周长是
,因而梯形的周长是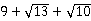 .
.
26.解:(1)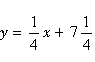 .
.
(2)当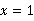 时,
时,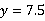 ,即加工完第一个零件是7点30分.
,即加工完第一个零件是7点30分.
(3)当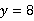 时,
时,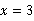 ,即8点整他加工完3个零件.
,即8点整他加工完3个零件.
(4)当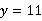 时,
时,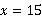 ,即上午他可加工完15个零件.
,即上午他可加工完15个零件.
27.解:(1)如图:B′(3,5),C′(5,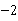 ).
).

(2)结合图形观察以上三组点的坐标可知坐标平面内任一点P(m,n)关于第一、三象限的角平分线 的对称点P′的坐标为(n,m).
的对称点P′的坐标为(n,m).
28.解:设原计划生产小麦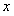 吨,生产玉米
吨,生产玉米 吨,
吨,
根据题意,得
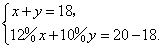 解得
解得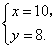
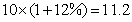 (吨),
(吨),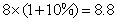 (吨).
(吨).
答:该专业户去年实际生产小麦11.2吨,玉米8.8吨.
29.解:如图,过点A作AC⊥ 轴于点C,
轴于点C,
则AC=3,OC=4,所以OA=OB=5,
故B点坐标为(0,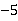 ).
).
设直线AO的关系式为 ,因为其过点A(4,3),
,因为其过点A(4,3),
则 ,解得
,解得 .所以
.所以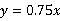 .
.
 设直线AB的关系式为
设直线AB的关系式为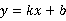 ,
,
因为其过点A(4,3)、B(0,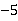 ),
),
则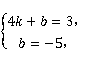 解得:
解得:
所以关系式为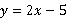 .
.
令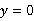 ,得
,得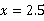 ,则D点坐标为(2.5,0).
,则D点坐标为(2.5,0).
所以两直线与 轴围成的三角形AOD的面积为2.5×3÷2=3.75.
轴围成的三角形AOD的面积为2.5×3÷2=3.75.
30.解:(1)从表中数据可知众数为113千瓦时,
平均数=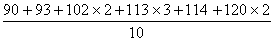 =108(千瓦时).
=108(千瓦时).
(2)某月耗电量Q=108×30=3 240(千瓦时).
(3)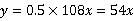 .
.
答:(1)上表中数据的众数为113千瓦时,平均数为108千瓦时;
(2)该校一个月的耗电量为3 240千瓦时;
(3)当地每千瓦时电的价格是0.5元时,该校应付电费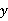 (元)与天数
(元)与天数 的函数关系式为
的函数关系式为
tag: 测试题 数学 初二数学试题,八年级数学试题,初中数学学习方法,初中学习 - 初二学习 - 初二数学 - 初二数学试题
相关分类
初二数学试题 推荐