12-20 22:52:45 浏览次数:941次 栏目:高考数学复习
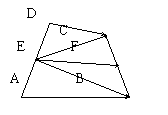
例1 .已知任意四边形ABCD的边AD和BC的中点分别为E、F,
求证: .
.
分析:构造三角形,利用向量的三角形法则证明.
证明:如图,连接EB和EC ,
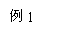 由
由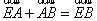 和
和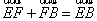 可得,
可得,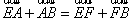 (1)
(1)
由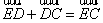 和
和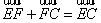 可得,
可得,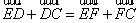 (2)
(2)
(1)+(2)得,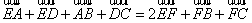 (3)
(3)
∵E、F分别为AD和BC的中点,∴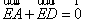 ,
,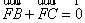 ,
,
代入(3)式得,
点拨:运用向量加减法解决几何问题时,需要发现或构造三角形或平行四边形.
例2.已知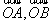 不共线,
不共线,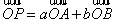 ,求证:A,P,B三点共线的充要条件是
,求证:A,P,B三点共线的充要条件是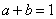
分析:证明三点共线可以通过向量共线来证明.
解:先证必要性:若A,P,B三点共线,则存在实数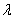 ,使得
,使得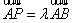 ,即
,即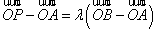 ,∴
,∴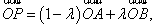 ∵
∵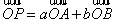 ,∴
,∴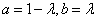 ,∴
,∴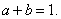
再证充分性:若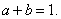 则
则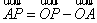 =
=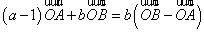 =
=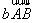 ,∴
,∴
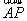 与
与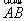 共线,∴A,P,B三点共线.
共线,∴A,P,B三点共线.
点拨:向量共线定理是向量知识中的一个基本定理,通常可以证明三点共线、直线平行等问题.
【反馈练习】
1.已知向量a和b反向,则下列等式成立的是(C)
A. |a|-|b|=|a-b| B. |a|-|b|=|a+b| C.|a|+|b|=|a-b| D. |a|+|b|=|a+b|
2.设四边形ABCD中,有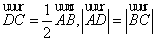 则这个四边形是(C)
则这个四边形是(C)
A.平行四边形 B.矩形 C.等腰梯形 D.菱形
3.设A、B、C、D、O是平面上的任意五点,试化简:
①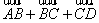
tag: 平面 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐