12-20 22:52:45 浏览次数:199次 栏目:高考数学复习
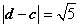 ,求
,求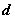
分析:本题主要考察向量及向量模的坐标表示和向量共线的充要条件.
解:(1)由题意得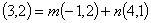
所以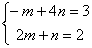 ,得
,得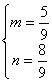
(2)
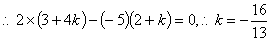
(3)设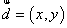 ,则
,则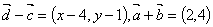
由题意得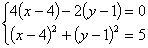
得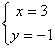 或
或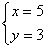 ∴
∴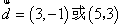
点拨:根据向量的坐标运算法则及两个向量平等行的充要条件、模的计算公式,建立方程组求解。
例2.已知△ABC的顶点分别为A(2,1),B(3,2),C(-3,-1),BC边上的高为AD,求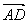 及点D的坐标、
及点D的坐标、
分析:注意向量坐标法的应用,及平行、垂直的充要条件.
解:设点D的坐标为(x,y)
∵AD是边BC上的高,
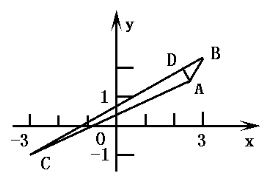
∴AD⊥BC,∴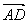 ⊥
⊥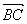
又∵C、B、D三点共线,
∴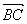 ∥
∥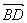
又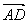 =(x-2,y-1),
=(x-2,y-1),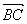 =(-6,-3)
=(-6,-3)
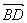 =(x-3,y-2)
=(x-3,y-2)
 ∴
∴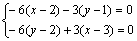
解方程组,得x=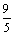 ,y=
,y=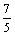
∴点D的坐标为(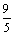 ,
,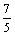 ),
),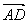 的坐标为(-
的坐标为(-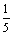 ,
,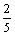 )
)
点拨:在解题中要注意综合运用向量的各种运算解决问题.
www.170xue.com
例3.已知向量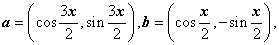 且
且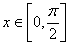
求(1)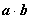
tag: 平面 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐