12-20 22:53:02 浏览次数:583次 栏目:高考数学复习
(1)讨论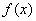 的奇偶性;
的奇偶性;
(2)若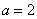 时,求
时,求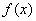 的最小值.
的最小值.
分析:去绝对值.
解:(1)当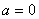 时,函数
时,函数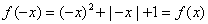
此时,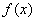 为偶函数.
为偶函数.
当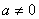 时,
时,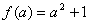 ,
,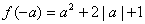 ,
,
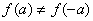 ,
,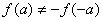 .
.
此时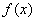 既不是奇函数,也不是偶函数.
既不是奇函数,也不是偶函数.
(2)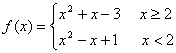
由于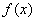 在
在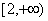 上的最小值为
上的最小值为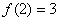 ,在
,在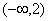 内的最小值为
内的最小值为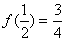 .
.
故函数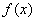 在
在 内的最小值为
内的最小值为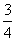 .
.
点评:注意分类讨论;分段函数求最值,先求每个区间上的函数最值,再确定最值中的最值.
例2.函数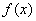
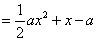
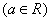 在区间
在区间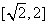 的最大值记为
的最大值记为 ,求
,求 的表达式.
的表达式.
分析:二次函数在给定区间上求最值,重点研究其在所给区间上的单调性情况.
解:∵直线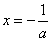 是抛物线
是抛物线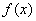
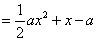 的对称轴,∴可分以下几种情况进行讨论:
的对称轴,∴可分以下几种情况进行讨论:
(1)当 时,函数
时,函数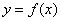 ,
, 的图象是开口向上的抛物线的一段,
的图象是开口向上的抛物线的一段,
由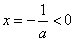
tag: 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐