12-20 22:53:02 浏览次数:476次 栏目:高考数学复习
②若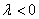 ,则
,则 ,
,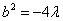
∴准线方程为: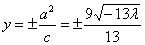 ,∴
,∴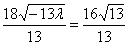 ,∴
,∴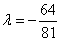
∴所求双曲线方程为: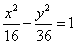 或
或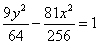
点拨:求圆锥曲线方程时,一般先由条件设出所求方程,然后再根据条件列出基本的方程组解方程组得出结果.
例2.已知点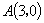 ,
,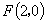 ,在双曲线
,在双曲线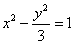 上求一点
上求一点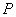 ,使
,使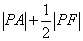 的值最小.
的值最小.
解:∵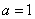 ,
,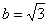 ,∴
,∴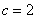 ,∴
,∴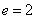
设点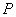 到与焦点
到与焦点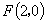 相应准线的距离为
相应准线的距离为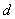 则
则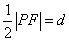
∴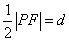 ,∴
,∴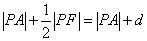
至此,将问题转化成在双曲线上求一点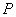 ,
,
使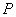 到定点
到定点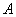 的距离与到准线距离和最小.
的距离与到准线距离和最小.
即到定点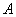 的距离与准线距离和最小为直线
的距离与准线距离和最小为直线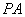 垂直于准线时,
垂直于准线时,
解之得,点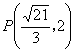 .
.
点拨:灵活巧妙地运用双曲线的比值定义于解题中,将会带给我们意想不到的方便和简单.教学中应着重培养学生灵活运用知识的能力.
【反馈练习】
1.若双曲线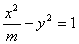 上的点到左准线的距离是到左焦点距离的
上的点到左准线的距离是到左焦点距离的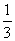 ,则
,则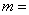
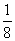
tag: 圆锥曲线 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐