12-20 22:53:02 浏览次数:761次 栏目:高考数学复习
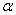 等于多少时,这个扇形的面积最大?最大面积是多少?
等于多少时,这个扇形的面积最大?最大面积是多少?
分析:选取变量,建立目标函数求最值.
解:设扇形的半径为x㎝,则弧长为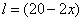 ㎝,故面积为
㎝,故面积为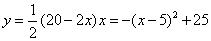 ,
,
当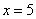 时,面积最大,此时
时,面积最大,此时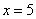 ,
,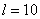 ,
,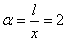 ,
,
所以当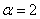 弧度时,扇形面积最大25
弧度时,扇形面积最大25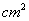 .
.
点评:由于弧度制引入,三角函数就可以看成是以实数为自变量的函数.
www.170xue.com【反馈演练】
1.若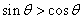 且
且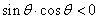 则
则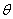 在第_
在第_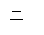 __象限.
__象限.
2.已知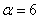 ,则点
,则点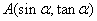 在第_
在第_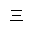 _象限.
_象限.
3.已知角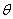 是第二象限,且
是第二象限,且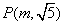 为其终边上一点,若
为其终边上一点,若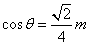 ,则m的值为_
,则m的值为_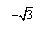 _.
_.
4.将时钟的分针拨快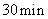 ,则时针转过的弧度为
,则时针转过的弧度为 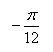 .
.
5.若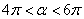 ,且
,且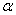 与
与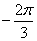 终边相同,则
终边相同,则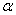 =
= 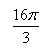 .
.
6.已知1弧度的圆心角所对的弦长2,则这个圆心角所对的弧长是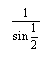 __,这个圆心角所在的扇形的面积是___
__,这个圆心角所在的扇形的面积是___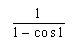 _.
_.
7.(1)已知扇形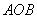 的周长是6cm,该扇形中心角是1弧度,求该扇形面积.
的周长是6cm,该扇形中心角是1弧度,求该扇形面积.
(2)若扇形的面积为8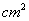 ,当扇形的中心角
,当扇形的中心角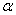
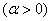
tag: 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐