12-20 22:58:55 浏览次数:359次 栏目:高考数学复习
2013高考数学复习:算法初步与框图(二)
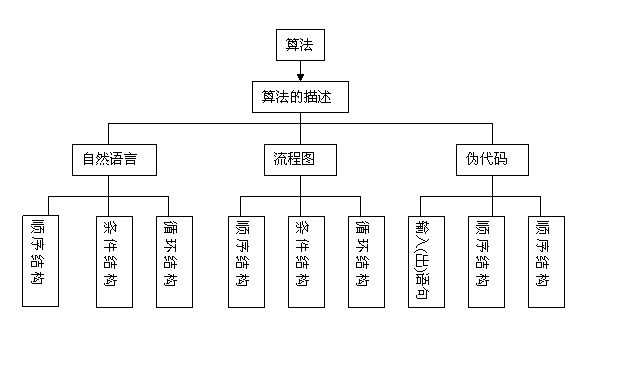
【知识图解】
 【方法点拨】
【方法点拨】
1.学习算法要理解算法的含义.明确建立算法就是设计完成一件事的操作步骤.一般地说,这样的操作步骤应该具有通用性,能处理一类问题.
2.掌握算法的三种基本结构.顺序结构、条件结构和循环结构是算法的三种基本结构.要通.具体实例了解三种基本结构的使用范围,通过流程图认识它们的基本特征.
3.掌握流程图的画法.用流程图表示算法具有、清晰的特点,也是高考重点考查的内容,要予以重视.特别是循环结构的流程图,对判断框中的条件与前测试还是后测试之间的关系一定要弄清楚.
4.熟悉建立算法的基本操作程序.建立算法的操作程序一般为:先探寻解决问题的方法,并用通俗的语言进行表述,再将通俗的算法语言用流程图直观表示,最后根据流程图选择适当的算法语句用伪代码表示算法过程.
第2课 流程图
【考点导读】
了解常用流程图符号的意义,能用流程图表示顺序,选择,循环这三种基本结构,并能识别简单的流程图所描述的算法.高考要求对流程图有最基本的认识,并能解决相关的简单问题.
【基础练习】
1.算法的三种基本结构是顺序结构、选择结构、循环结构 .
2.流程图中表示判断框的是菱形框 .
3.根据题意,完成流程图填空:
这是一个输入两个数,输出这两个数差的绝对值的一个算法.请将空格部分填上适当的内容(1)a>b;(2)b-a
【范例解析】
例1.已知梯形的上底、下底和高分别为5、8、9,写出求梯形的面积的算法,画出流程图.
解算法如下
S1 a←5;
S2 b←8;
S3 h←9;
S4 S←(a+b)×h/2;
S5 输出S.
流程图为:
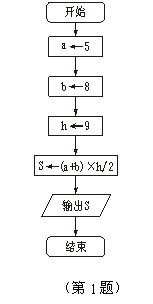
点评 本题中用的是顺序结构是最简单的算法结构,是任何一个算法都离不开的基本结构.
www.170xue.com例2 .设计求解不等式ax+b>0(a≠0)的一个算法,并用流程图表示.
解:第一步 输入a,b;
第二步 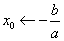
第三步 若a>0,那么输出x>x0,否则输出x
流程图为:
点评 解决此类不等式问题时,因涉及到对一次项系数的讨论一般采用条件结构设计算法.
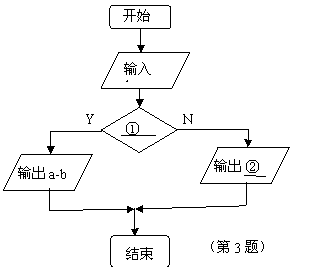
【反馈演练】
1.如图表示的算法结构是 顺序 结构.
2.下面的程序执行后的结果是 4,1 .
解析:由题意得
3输入x的值,通过函数y=
① x
② 1≤x<10
③ 3x-11
4 如图所示,给出的是计算
5. 给出以下一个算法的程序框图(如图所示).该程序框图的功能是 求出a,b,c三数中的最小数 .
6.根据下面的算法画出相应的流程图.
算法:
S1 T←0;
S2 I←2;
S3 T←T+I;
S4 I←I+2;
S5 如果I不大于200,转S3;
S6 输出T.
答案:解:这是计算2+4+6+…+200的一个算法.
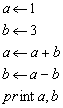
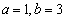 ,故执行到第三步时,把
,故执行到第三步时,把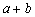 的值给
的值给 ,这时
,这时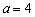 ,第四步,把
,第四步,把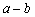 的值给
的值给 ,这时
,这时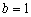 .
.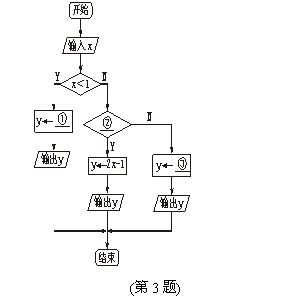
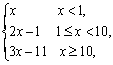 求出y的值,现给出此算法流程图的一部分,请将空格部分填上适当的内容
求出y的值,现给出此算法流程图的一部分,请将空格部分填上适当的内容 的值的一个程序框图,其中判断框内应填入的条件是i>20 .
的值的一个程序框图,其中判断框内应填入的条件是i>20 .

,2017高考数学复习:算法初步与框图(二)
tag: 高考数学 高考数学复习,高考数学复习大全,高考复习方法,高中学习 - 高考学习 - 高考数学复习资料 - 高考数学复习
相关分类
高考数学复习 推荐