12-20 22:52:45 浏览次数:867次 栏目:高考备考
 的方程;
的方程;
(Ⅱ)证明函数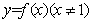 的图象在直线
的图象在直线 的下方;
的下方;
(Ⅲ)讨论函数 零点的个数.
零点的个数.
19.(本小题共14分)
已知椭圆的中心在原点,焦点在 轴上,离心率为
轴上,离心率为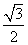 ,且经过点
,且经过点 ,直线
,直线 交椭圆于不同的两点
交椭圆于不同的两点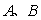 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)求 的取值范围;
的取值范围;
(Ⅲ)若直线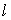 不过点
不过点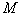 ,求证:直线
,求证:直线 的斜率互为相反数.
的斜率互为相反数.
20.(本小题共13分)
定义:如果数列 的任意连续三项均能构成一个三角形的三边长,则称
的任意连续三项均能构成一个三角形的三边长,则称 为“三角形”数列.对于“三角形”数列
为“三角形”数列.对于“三角形”数列 ,如果函数
,如果函数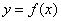 使得
使得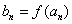 仍为一个“三角形”数列,则称
仍为一个“三角形”数列,则称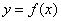 是数列
是数列 的“保三角形函数”
的“保三角形函数” .
.
(Ⅰ)已知 是首项为
是首项为 ,公差为
,公差为 的等差数列,若
的等差数列,若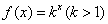 是数列
是数列 的“保三角形函数”,求
的“保三角形函数”,求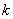 的取值范围;
的取值范围;
(Ⅱ)已知数列 的首项为
的首项为 ,
, 是数列
是数列 的前n项和,且满足
的前n项和,且满足 ,证明
,证明 是“三角形”数列;
是“三角形”数列;
(Ⅲ)若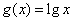
相关分类
高考备考 推荐