12-20 22:58:55 浏览次数:202次 栏目:高考备考
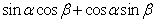 =
=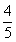
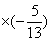 +
+
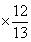 =
=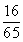 .……………7分
.……………7分
(Ⅱ)方法(1)∵∣AB∣=|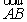 |=|
|=|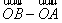 |,…………………………9分
|,…………………………9分
又∵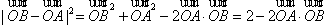 ,…………11分
,…………11分
∴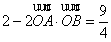 ,
,
∴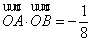 .……………………………………13分
.……………………………………13分
方法(2)∵ , …………………10分
, …………………10分
∴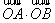 =
=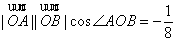 . ………………………………… 13分
. ………………………………… 13分
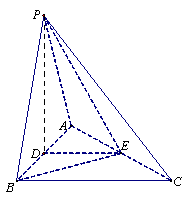
17.
解:(Ⅰ) D、E分别为AB、AC中点,\DE//BC .
D、E分别为AB、AC中点,\DE//BC .
 DE?平面PBC,BC?平面PBC,
DE?平面PBC,BC?平面PBC,
\DE//平面PBC .…………………………4分
(Ⅱ)连结PD,
 PA=PB,
PA=PB,
 PD
PD 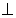 AB. …………………………….5分
AB. …………………………….5分
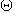
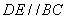 ,BC
,BC 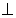 AB,
AB,
 DE
DE 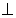 AB..... .........................................6分
AB..... .........................................6分
又
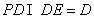 ,
,
 AB
AB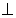 平面PDE.................................................8分
平面PDE.................................................8分
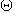 PE?平面PDE,
PE?平面PDE,
 AB
AB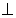 PE . ................................................9分
PE . ................................................9分
(Ⅲ)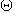 平面PAB
平面PAB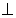 平面ABC,平面PAB
平面ABC,平面PAB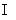 平面ABC=AB,PD
平面ABC=AB,PD 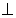 AB,
AB,
 PD
PD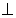 平面ABC..............................10分
平面ABC..............................10分
如图,以D为原点建立空间直角坐标系

 B(1,0,0),P(0,0,
B(1,0,0),P(0,0,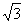 ),E(0,
),E(0,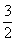 ,0) ,
,0) ,

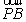 =(1,0,
=(1,0,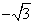 ),
), =(0,
=(0, 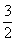 ,
, 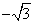 ).
).
设平面PBE的法向量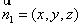 ,
,

 令
令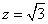
得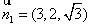 . ............................11分
. ............................11分
 DE
DE 平面PAB,
平面PAB,
 平面PAB的法向量为
平面PAB的法向量为 .………….....................12分
.………….....................12分
设二面角的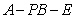 大小为
大小为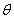 ,
,
由图知,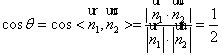 ,
,
所以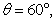 即二面角的
即二面角的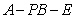 大小为
大小为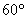 . ..........................................14分
. ..........................................14分
18.
解:(Ⅰ)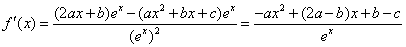 ........2分
........2分
令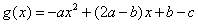 ,
,
因为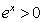 ,所以
,所以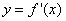 的零点就是
的零点就是 的零点,且
的零点,且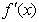 与
与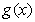 符号相同.
符号相同.
又因为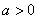 ,所以
,所以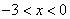 时,g(x)>0,即
时,g(x)>0,即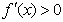 , ………………………4分
, ………………………4分
当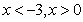 时,g(x)<0 ,即
时,g(x)<0 ,即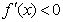 , …………………………………………6分
, …………………………………………6分
所以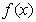 的单调增区间是(-3,0),单调减区间是(-∞,-3),(0,+∞).……7分
的单调增区间是(-3,0),单调减区间是(-∞,-3),(0,+∞).……7分
(Ⅱ)由(Ⅰ)知,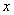 =-3是
=-3是 的极小值点,所以有
的极小值点,所以有
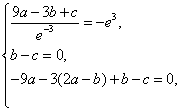
解得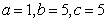 , ………………………11分
, ………………………11分
所以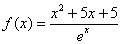 .
.
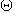
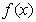 的单调增区间是(-3,0),单调减区间是(-∞,-3),(0,+∞),
的单调增区间是(-3,0),单调减区间是(-∞,-3),(0,+∞),

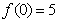 为函数
为函数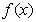 的极大值, ………………………………12分
的极大值, ………………………………12分

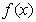 在区间
在区间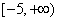
 上的最大值取
上的最大值取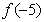 和
和 中的最大者. …………….13分
中的最大者. …………….13分
而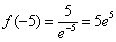 >5,所以函数f(x)在区间
>5,所以函数f(x)在区间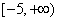 上的最大值是
上的最大值是 ..…14分
..…14分
编辑推荐:
查看更多有关高考数学的内容,请点击>>高考数学知识点专题
www.170xue.com
19.解:(Ⅰ)设C1的方程为
 ,C2的方程为
,C2的方程为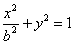 ,其中
,其中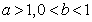 ...2分
...2分
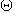 C1 ,C2的离心率相同,所以
C1 ,C2的离心率相同,所以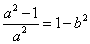 ,所以
,所以 ,……………………….…3分
,……………………….…3分
 C2的方程为
C2的方程为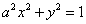 .
.
当m=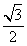 时,A
时,A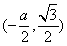 ,C
,C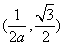 . .………………………………………….5分
. .………………………………………….5分
又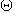
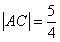 ,所以,
,所以, ,解得a=2或a=
,解得a=2或a=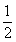 (舍), ………….…………..6分
(舍), ………….…………..6分
 C1 ,C2的方程分别为
C1 ,C2的方程分别为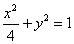 ,
,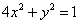 .………………………………….7分
.………………………………….7分
(Ⅱ)A(- ,m), B(-
,m), B(- ,m) . …………………………………………9分
,m) . …………………………………………9分
 OB∥AN,
OB∥AN,
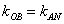 ,
,

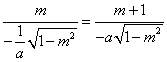 ,
,
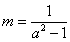 . …………………………………….11分
. …………………………………….11分
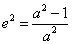 ,?
,?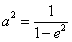 ,
,
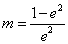 . ………………………………………12分
. ………………………………………12分
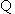
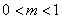 ,?
,? ,?
,?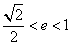 .........................................................13分
.........................................................13分
20.
解:(Ⅰ) ?B
?B
 直线B
直线B
由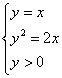 得
得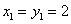 ,即点A1的坐标为(2,2),进而得
,即点A1的坐标为(2,2),进而得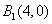 .…..3分
.…..3分
(Ⅱ)根据 和
和 分别是以
分别是以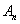 和
和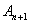 为直角顶点的等腰直角三角形可
为直角顶点的等腰直角三角形可
得 ,即
,即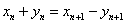 .(*) …………………………..5分
.(*) …………………………..5分

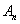 和
和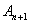 均在曲线
均在曲线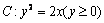 上,
上,
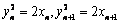 ,
,

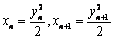 ,代入(*)式得
,代入(*)式得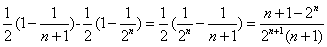 ,
,

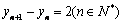 , ………………………………………………………..7分
, ………………………………………………………..7分
 数列
数列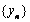 是以
是以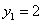 为
为 首项,2为公差的等差数列,
首项,2为公差的等差数列,
 其通项公式为
其通项公式为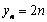 (
(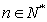 ). ……………………………………………....8分
). ……………………………………………....8分
(Ⅲ)由(Ⅱ)可知,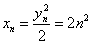 ,
,

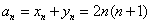 , ……………………………………………………9分
, ……………………………………………………9分

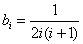 ,
,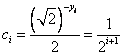 .
.

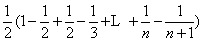
=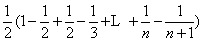 =
=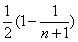 .………..…………10分
.………..…………10分
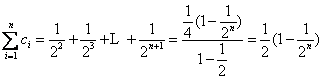 ……………………….11分
……………………….11分
(方法一)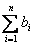 -
-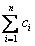 =
=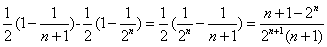 .
.
当n=1时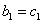 不符合题意,
不符合题意,
当n=2时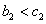 ,符合题意,
,符合题意,
猜想对于一切大于或等于2的自然数,都有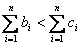 .(
.(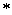 )
)
观察知 ,欲证(
,欲证(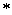 )式,只需证明当n≥2时,
)式,只需证明当n≥2时, n+1<2n
n+1<2n
以下用数学归纳法证明如下:
(1)当n=2时,左边=3,右边=4,左边<右边;
(2)假设n=k(k≥2)时,(k+1)<2k,
当n=k+1时,左边=(k+1)+1<2k+1<2k+2k=2k+1=右边,
 对于一切大于或等于2的正整数,都有n+1<2n,即
对于一切大于或等于2的正整数,都有n+1<2n,即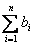 <
<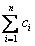 成立.
成立.
综上,满足题意的n的最小值为2. ……………………………………………..13分
(方法二)欲证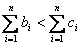 成立,只需证明当n≥2时,n+1<2n.
成立,只需证明当n≥2时,n+1<2n.
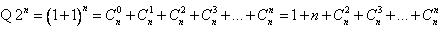 ,
,
并且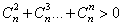 ,
,
 当
当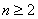 时,
时, .
.
编辑推荐:
查看更多有关高考数学的内容,请点击>>高考数学知识点专题
,丰台区高三上册数学理科试卷及答案相关分类
高考备考 推荐