阜阳十中九年级上期末数学试卷及答案

∵OA=OC，∴∠ACP=CAO=300，∴∠AOP=600，

又∵AP=AC.∴∠P=∠ACP=300，∴∠OAP=900，即OA⊥AP，

∴AP是⊙O的切线；

(2) CD是⊙O的直径，连接AD，∴∠CAD=900，

∴AD=AC?tan300=.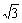

∵∠ADC=∠B=600，∴∠PAD=∠ADC-∠P=300，∴∠P=∠PAD，

∴PD=AD=.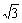

 24解：(1)由题意，得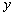：＝200＋（80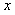－）·20＝－20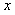＋1800，

             ∴销售量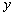件与销售单价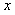元之间的函数关系式为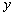：＝－20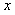＋1800。

            (2) 由题意，得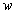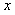：＝（－60）（－20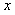＋1800）＝－20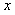2＋3000 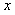－108000，

         ∴利润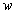元与销售单价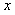元之间的函数关系式为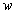：＝－20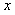2＋3000 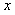－108000。

        (3) 由题意，得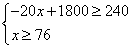：，解得76≤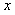≤78。

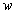           对于＝－20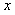2＋3000 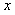－108000，对称轴为＝，

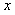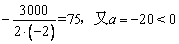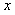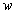          ∴当76≤≤78时，随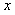增大而减小。

          ∴当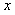＝76时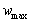，＝（76－60）（－20×76＋1800）＝4480。

          ∴商场销售该品牌童装获得的最大利润是4480元。

上一页  [1] [2] [3] [4]