12-20 22:59:40 浏览次数:596次 栏目:中考试题
 的长;
的长;
(2)如图②,过点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 ,当点
,当点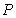 、
、 在移动的过程中,线段
在移动的过程中,线段 、
、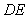 、
、 中是否存在长度保持不变的线段?如存在,请求出不变线段的长度。
中是否存在长度保持不变的线段?如存在,请求出不变线段的长度。
(3)如图③,△ABC的中线AM与中线BN相交于点G,当PQ过点G时,求BP的长。


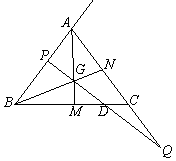
图① 图② 图③
四、(本题12分)
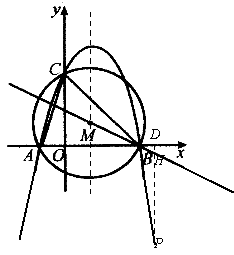
28.如图,抛物线
(1)求这条抛物线的解析式;
(2)求△ABC外接圆的圆心M的纵坐标;
(3)在抛物线上是否存在一点P,使△PBD(PD垂直于x轴,垂足为D)被直线BM分成的面积比为1:2两部分?若存在,请求出点P的坐标;若不存在,请说明理由。
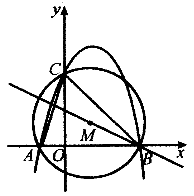
参考答案:
一、选择(每题3分,共30分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | B | D | A | A | B | C | C | D | C |
二、填空题(每题3分,共12分)
11、 12、
12、 13、 4 14、
13、 4 14、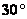
三、解答题(本大题2个小题,共18分)
15.计算:(1)(本小题6分)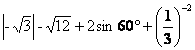
解: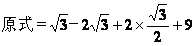 ………………………4分
………………………4分
=9 …………………………………………6分
(2)(本小题6分)解方程: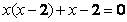
解: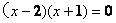 ……………………3分
……………………3分

 ……………………6分
……………………6分
(其他解法也可,相应给分)
16.(本小题6分)解:过C作CD⊥AB,垂足为D,设CD=x………………(1分)
由题意∠CAB=30°,∠CBD=60°
∵在Rt△ACD中,∠CAB=30°,∴AD=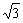 x
x
 ∵在Rt△BCD中,∠CBD=60°,∴BD=
∵在Rt△BCD中,∠CBD=60°,∴BD= …………(3分)
…………(3分)
又∵AD=AB+BD,∴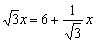
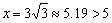 ………………………(5分)
………………………(5分)
∴无触礁的危险…………………………(6分)
www.170xue.com四、解答题(本题8分)
17.(1)证:∵菱形ABCD
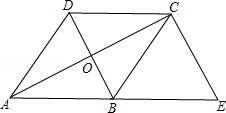 ∴AB∥CD,AB=CD ………………(1分)
∴AB∥CD,AB=CD ………………(1分)
又∵BE=AB
∴CD=BE,CD∥BE ……………(2分)
∴四边形BECD是平行四边形………(3分)
∴BD=EC ……………………………(4分)
(2)解:∵菱形ABCD
∴BD⊥AC …………………………(5分)
又∵CE∥BD
∴∠ACE=90°……………………(6分)
∵∠E=55°,∴∠ACB=35°,AB=BC
∴∠BAO=35°………………………(8分)
五、解答题(本大题2个小题,共18分)
18.(本小题8分)
解:(1)用列表法表示(x,y)所有可能出现的结果如下:(树状图列完整也可)………………(4分)
| x\y | -2 | -1 | 1 |
| -2 | (-2,-2) | (-2,-1) | (-2,1) |
| -1 | (-1,-2) | (-1,-1) | (-1,1) |
| 1 | (1,-2) | (1,-1) | (1,1) |
(2)∵(x,y)所有可能出现的结果共有9种情况,点 在
在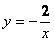 图象上的有2种,所以出现的概率是
图象上的有2种,所以出现的概率是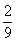 ………………(8分)
………………(8分)
19.(本小题10分)
解:(1)∵点C(4,-1)在反比例函数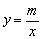 的图象上,
的图象上,
∴ ,∴m=-4,…………………………(1分)
,∴m=-4,…………………………(1分)
∴反比例函数的解析式为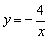
∵点D在反比例函数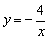 的图象上,且DE=2
的图象上,且DE=2
∴ ,∴x=-2,∴点D的坐标为(-2,2)…………………………(4分)
,∴x=-2,∴点D的坐标为(-2,2)…………………………(4分)
∵C、D两点在直线y=kx+b上,∴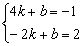
解得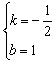 ∴一次函数的解析式为
∴一次函数的解析式为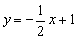 ……………………(6分)
……………………(6分)
(2)当x<-2或0
 六、解答题(本题10分)
六、解答题(本题10分)
20.(1)连结OB …………………………(1分)
∵BC=CE ∴∠CBE=∠CEB
∵OA=OB ∴∠OAB=∠OBA
∵CD⊥OA ∴∠OAB+∠AED=90°
∴∠CBO=90°…………………………(2分)
∵B在圆上 ∴BC是圆的切线 ………(3分)
(2)连结OF………………………………(4分)
 ∵DC是OA的垂直平分线 ∴OA=OF=AF
∵DC是OA的垂直平分线 ∴OA=OF=AF
∴∠AOF=60°……………………………(5分)
∴∠ABF=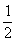 ∠AOF=30°………………(6分)
∠AOF=30°………………(6分)
(3)作CM⊥AB于M ……………………………(7分)
∵BC=CE,BE= ,∴ME=MB=
,∴ME=MB= BE=
BE=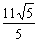
∵tan∠OAB= , ∵∠OAB=∠MCE
, ∵∠OAB=∠MCE
∵t an∠MCE=
an∠MCE=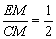 ,∴CM=2EM=
,∴CM=2EM=

∴CE= ,
,
∵CD=13,∴DE=2………(8分)
∵△ADE∽△CME,∴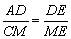
∴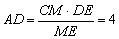 …………………(9分)
…………………(9分)
∵D是OA的中点,∴半径OA=8………………………………………………(10分)
www.170xue.comB卷(50分)
21、 2012 22、 23、 5,-3 24、 4 25、
23、 5,-3 24、 4 25、
26、解:(1)800×200=160000(元)。………………………………………(2分)
(2)依题意(图),设
 ,
, ,则有
,则有
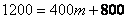 ,
, ,解得
,解得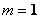 ,
,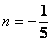 。
。
∴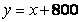 ,
, 。……………………
。…………………… ……(5分)
……(5分)
(3)∵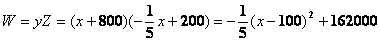
∴要使该商场销售热水器的总收益W(元)最大,政府应将每台补贴款额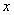 定为100元,其总收益W的最大值为162000元。…………………………(8分)
定为100元,其总收益W的最大值为162000元。…………………………(8分)
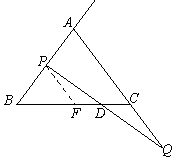 三、(本题10分)
三、(本题10分)
27、(1)过P作PF∥AC交BC于F……………(1分)
∵AB=AC,BP=CQ
∴PB=PF=CQ
∴△PFD≌△QCD(AAS)
CD=FD …………………(2分)
∵P是AB的中点,
∴F是BC 的中点, CD=
的中点, CD=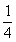 BC=
BC= …………(3分)
…………(3分)
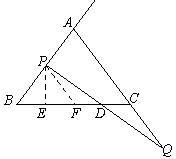 (2)DE长度保持不变。理由如下:…………(4分)
(2)DE长度保持不变。理由如下:…………(4分)
过P作PF∥AC交BC于点F,则………(5分)
由(1)△PFD≌△QCD(AAS),PE⊥BC
BE=EF, DF=DC
∴DE=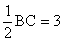 ……(6分)
……(6分)
(3)连MN,过P作PI⊥BC于点 …………………………………………………(7分)
∵AM、BN是△ABC的中线,∴MN平行且等于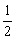 AB,
AB,
∵AB=AC,
 ,BC=6,∴AM=4
,BC=6,∴AM=4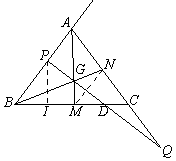
∴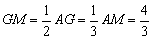
设BI=3k,则PI=4k, BP=5k, 由△DMG∽△DIP有:
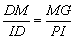 由(2)知ID=3 即
由(2)知ID=3 即 
MD= -------------9分
-------------9分
又∵BM=BI+IM=ID=IM+MD=3 ∴BI=MD 即
∴ ,
,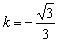 (舍去)
(舍去)
∴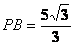 …………
………… ……(10分)
……(10分)
四、(本题12分)
28.解:(1)∵C(0,3),又∵抛物线顶点横坐标为1,∴抛物线对称轴x=1
 ∵AB=4,∴A(-1,0),B(3,0)
∵AB=4,∴A(-1,0),B(3,0)
∴y=a(x+1)(x-3)过C(0,3)
∴a= -1
∴y=-x2+2x+3 …………………………(3分)
(2)△ABC的外心M在对称轴x=1上
∴设M(1,b)
MC=MB,MC2=MB2
12+(3-b)2=22+b2
∴b=1
 ∴圆心M的纵坐标为1。…………………………………………(7分)
∴圆心M的纵坐标为1。…………………………………………(7分)
(3)当P在直线BM上方时,设P(x,-x2+2x+3)
直线MB: …………
………… ……(8分)
……(8分)
(ⅰ)当S△HDB:S△PHB=1:2时,
HD:PH=1:2, HD:PH=1:3

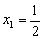 ,x2=3(舍去)
,x2=3(舍去)
∴ …………………………………………(9分)
…………………………………………(9分)
(ⅱ)当S△HDB:S△PHB=2:1时,HD:PH=2:3
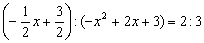
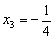 ,x4=3(舍去)
,x4=3(舍去)
∴ …………………………………………(10分)
…………………………………………(10分)
(ⅲ)当P在直线BM下方时,P(x,-x2+2x+3)
 S△HDB:S△PHB=1:2时,
S△HDB:S△PHB=1:2时,
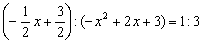
∴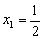 ,
, (舍去)
(舍去)
同理当S△HDB:S△PHB=2:1时,
 (舍去)……………(11分)
(舍去)……………(11分)
综上,存在满足条件的点P的坐标为
 ,
, ……………………(12分)
……………………(12分)
相关分类
中考试题 推荐