迎春杯五年级组试题详解

标签：五年级数学题,五年级数学应用题,小学五年级数学试卷,http://www.170xue.com 迎春杯五年级组试题详解,http://www.170xue.com

2010年“数学解题能力展示”五年级组初试试卷

试题解析

一、填空题I

1、  计算：6x(1/2—1/3)+12x(1/3+1/4)+19—33+21—7+22=（  30  ）

解析：整数分数混合计算，较简单，先通分，算出括号内数值即可。

 

 

2、  小张有200支铅笔，小李有20支钢笔，每次小张给小李6支铅笔，小李还给小张1支钢笔，经过____________次这样的交换后，小张手中铅笔的数量是小李手中钢笔数量的11倍。

解析：假设经过N次变换，有200-6N=5×（20-N），得N=4

 

3、在长方形ABCD中，BE=5，EC=4，CF=4，FD=1，如图所示，那么△AEF的面积为（20）  

解析：用长方形面积剪掉周围三个三角形面积即可，得20.（或用梯形ＡＥＣＤ剪掉三角形ＥＣＦ和ＦＤＡ即可）

 

4、  2009x2009x……2009  的个位数字是__1____.

      2010个2009

解析：只需考虑个位数字9的乘方规律，9，1，9，1，……循环，为1。

 

一、填空题II

 

5、  一个等差数列的第3项是14，第18项是23，那么这个数列的前2010项中有__402__项是整数。

 

解析：a(3)=14,  a(18)=23 ,a(18)=a(3)+15d,得d=3/5,故每五个数中有一个为整数，2010÷5=402.

 

6、  甲、乙两车同时从A城市出发驶向距离300千米远的B城市。已知甲车比乙车晚出发1个小时，但提前1个小时到达B城市。那么，甲车在距离B城市__150__千米处追上乙车。

解析：150

                                            

7、  已知一个五位回文数等于45与一个四位回文数的乘积（即abcda =45xdeed）,那么这个五位回文数最大的可能值是__59895__。

解析：59895，从大数开始尝试即可，首位两个数必须为５才能被４５整除。

8、  请从1，2，3……，9，10中选出若干个数，使得1，2，3……，19，20这20个数中的每个数都等于某个选出的数或某两个选出的数（可以相等）的和。那么，至少需要选出__6__个数。

解析：6

二、填空题III

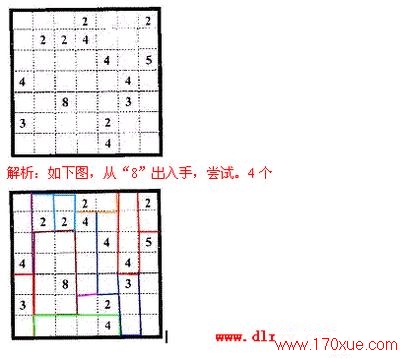
9、  如图，请沿虚线将7x7的方格表分割成若干个长方形，使得每个长方形中恰好包含一个数字，并且这个数字就是长方形的面积，那么第四列的7个小方格分别属于__4_ 个不同长方形。

10、  九个大小相等的小正方形拼成了右图。现从点A走到点B，每次只能沿着小正方形的对角线从一个顶点到另一个顶点，不允许走重复路线（如图的虚线就是一种走法），那么从点A走到点B共有__________ 种不同的走法。

 

（1）A—H—C—D—E—B

（2）Ａ－Ｈ－Ｇ－Ｆ－Ｅ－Ｂ

（３）Ａ－Ｈ－Ｃ－Ｄ－Ｅ－Ｈ－Ｇ－Ｆ－Ｅ－Ｂ

（４）Ａ－Ｈ－Ｇ－Ｆ－Ｅ－Ｈ－Ｃ－Ｄ－Ｅ－Ｂ

（５）Ａ－Ｈ－Ｃ－Ｄ－Ｅ－Ｆ－Ｇ－Ｈ－Ｅ－Ｂ

（６）Ａ－Ｈ－Ｇ－Ｆ－Ｅ－Ｄ－Ｃ－Ｈ－Ｅ－Ｂ

（７）Ａ－Ｈ－Ｅ－Ｄ－Ｃ－Ｈ－Ｇ－Ｆ－Ｅ－Ｂ

（８）Ａ－Ｈ－Ｅ－Ｆ－Ｃ－Ｈ－Ｃ－Ｄ－Ｅ－Ｂ

（９）Ａ－Ｈ－Ｅ－Ｂ

 

12、  如图，等腰直角三角形DEF的斜边在等腰直角三角形ABC的斜边上，连接AE、AD、AF，于是整个图形被分成五块小三角形。图中已标出其中三块的面积，那么△ABC的面积是__36___。

 

用燕尾定理，得Ｓ１＝２/5,S2=3/5,再由蝴蝶定理，BDE的面积=ADE的面积，所以BDM的面积=2+2/5=12/5,同理CDM的面积=18/5,而MD：DA=（２/5）：2=1：5，所以三角形ABD面积=5×BDM的面积，同理三角形ACD=5×CDM的面积，所以三角形ABC面积=6×BDC的面积=6×（12/5+18/5）=36

 

13、  如图，C，D为AB的三等分点；8点整时甲从A出发匀速向B行走，8点12分乙

从B出发匀速向A行走，再过几分钟后丙也从B出发匀速向A行走；甲，乙在C点相遇时丙恰好走到D点，甲，丙8：30相遇时乙恰好到A。那么，丙出发时是8点___16_____分。

 

WORD文档下载，迎春杯五年级组试题详解