12-20 22:52:45 浏览次数:236次 栏目:高考备考
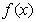 在区间
在区间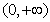 上单调,此时函数
上单调,此时函数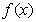 无最大值.
无最大值.
当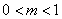 时,
时,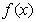 在区间
在区间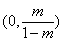 内单调递增,在区间
内单调递增,在区间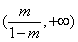 内单调递减,
内单调递减,
所以当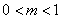 时函数
时函数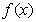 有最大值.
有最大值.
最大值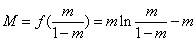 .
.
因为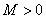 ,所以有
,所以有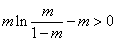 ,解之得
,解之得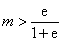 .
.
所以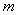 的取值范围是
的取值范围是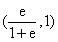 .
.
(19)(共13分)
(Ⅰ)解:由已知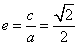 ,
,
所以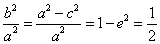 .
.
所以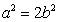 .
.
所以 :
: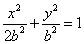 ,即
,即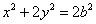 .
.
因为椭圆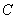 过点
过点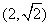 ,
,
得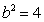 ,
,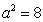 .
.
所以椭圆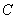 的方程为
的方程为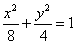 .
.
(Ⅱ)证明:由(Ⅰ)知椭圆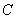 的焦点坐标为
的焦点坐标为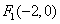 ,
,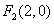 .
.
根据题意, 可设直线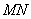 的方程为
的方程为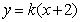 ,
,
由于直线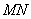 与直线
与直线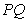
相关分类
高考备考 推荐