12-20 22:52:45 浏览次数:397次 栏目:高考备考
 www.170xue.com
www.170xue.com
(Ⅲ)若存在 阶完美数列,则由性质1易知
阶完美数列,则由性质1易知 中必有
中必有 个元素,由(Ⅱ)知
个元素,由(Ⅱ)知 中元素成对出现(互为相反数),且
中元素成对出现(互为相反数),且 ,又
,又 具有性质2,则
具有性质2,则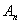 中
中 个元素必为
个元素必为
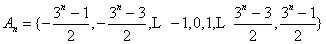 ,
,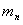
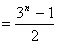 。
。
下面用数学归纳法证明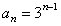
显然 时命题成立,假设当
时命题成立,假设当 (
( 时命题成立,即
时命题成立,即
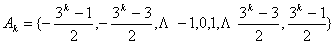
当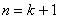 时,只需证
时,只需证
 由于对称性只写出了
由于对称性只写出了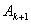 元素正的部分,其中
元素正的部分,其中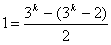
既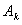 中正的部分的
中正的部分的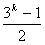 个元素统一为
个元素统一为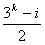 ,其中
,其中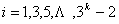
则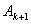 中从
中从 ,到
,到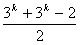 这
这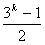 个元素可以用
个元素可以用 唯一表示,
唯一表示,
其中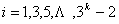 ,
,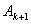 中从(
中从(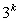 +1)到最大值
+1)到最大值 ,
,
相关分类
高考备考 推荐