福建师大附中高一上册数学期末试卷及答案

标签：高一数学试题大全,高一数学学习方法,http://www.170xue.com 福建师大附中高一上册数学期末试卷及答案,http://www.170xue.com

　　⊿BCD中 O、E分别为BD、BC中点

　　∴ OE∥CD 且

　　∴ 异面直线AB与C D所成角等于∠OEF（或其补角）

　　 又OF是Rt⊿AOC斜边上的中线　　 ∴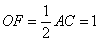

　　∴ 等腰⊿OEF中

www.170xue.com

　　24、(本小题满分10分)

　　解：圆C的方程可化为(x-a)²+(y-3a)²=4a

　　∴圆心为C（a，3a），半径为r=2　

　　（1）若a=2，则c(2，6)，r=，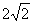

　　∵弦AB过圆心时最长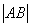，∴max=4　

　　（2）若m=2，则圆心C（a，3a）到直线x-y+2=0的距离d=，r=2直线与圆相交，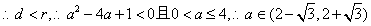　

　　又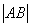=2，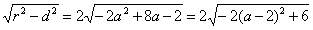

　　∴当a=2时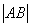，max=2，　

　　（3）圆心C（a，3a）到直线x-y+m=0的距离d=

　　∵直线L是圆心C的切线，∴d=r ，　 ，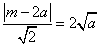　　

　　∴m=2a±　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　 　　

　　∵直线L是圆心C下方，　　 ∴m=2a-2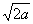=(-1)²-1

　　∵，∴当a=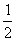时，m_min=-1;当a=4时，，m_max=8-4，故实数m的取值范围是[-1，8-4]　

　　附加题.（10分）

　　设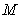点是圆上的动点，过点作圆的两条切线，切点分别为，切线

上一页  [1] [2] [3] [4] [5] [6] [7] [8]  下一页

，福建师大附中高一上册数学期末试卷及答案