12-20 22:52:45 浏览次数:467次 栏目:高考备考

 .
.
∴当 时,
时, 有最大值为
有最大值为 .
.
(3)解:由(2)知当 取得最大值时
取得最大值时 ,故
,故 ,
,
由(2)知 ,故
,故 是异面直线
是异面直线 与
与 所成的角.
所成的角.
在 中
中 ,
,
由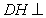 平面
平面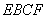 ,
, 平面
平面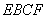 ,故
,故
 在
在 中
中
 ,
,
∴ .
.
∴异面直线 与
与 所成的角的余弦值为
所成的角的余弦值为 .
.
法二:(1)证明:∵平面 平面
平面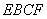 ,交线
,交线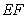 ,
, 平面
平面 ,
, ,故
,故 ⊥平面
⊥平面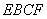 ,又
,又
上一页 [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] 下一页
,潮州市高三上册数学理科试卷及答案相关分类
高考备考 推荐